RESEÑA HISTORICA
Los numeros fueron llevados de la india a europa por los arabes.
LOS NUEROS REALES COMO UN CAMPO.
Axiomas de los números reales
Para que todos los procedimientos matemáticos usados sean válidos se debe partir de una base que respalde cada procedimiento, cada paso lógico usado, y debe, en consecuencia, demostrarse cada afirmación no trivial. Son estas demostraciones los pilares fundamentales de toda rama de las matemáticas, ya que sin ellos puede ponerse en duda la veracidad de cualquier afirmación.
Las afirmaciones a las que se hace referencia se llaman axiomas. Serán, por lo tanto, afirmaciones que se aceptan como verdaderas debido a su trivialidad, pudiendo en ocasiones ser demostradas cuando no lo son.
El otro tipo de afirmaciones a las que se hace referencia diciendo: "afirmación no trivial", son los teoremas, que son ya, afirmaciones no tan triviales y muchas veces poco intuitivas. Estas afirmaciones deben ser demostradas usando los axiomas u otros teoremas ya demostrados. Una consecuencia inmediata de un teorema se llamará corolario.
Hay tres tipos de axiomas:
- Los axiomas algebraicos
- Los axiomas de orden
- El axioma topológico
IN= {1,2,3,4.....}
NUMEROS ENTEROS
Z= {-3,-2,-1,0,1,2,3...}
NUMEROS FRACCIONARIOS
Q= {...-3.5,-3,,-2,-1,-1/2,0,1,1/2,2,3,3.5....}
NUMEROS REALES
INcZcQcR
NUMEROS IRRACIONALES
II= {V2,r,e }
MULTIPLOS Y DIVISORES
a,b,c, E Z, c= a.b <=> c es multiplo de a y b , Y ,ab son divisores de C.
20 = 4.5
-12 = -3 ( 4)
Número primo
En matemáticas, particularmente en Teoría de números o Aritmética, un número primo es unnúmero natural mayor que 1 que tiene únicamente dos divisores distintos: él mismo y el 1.1 2 Los números primos se contraponen así a los compuestos, que son aquellos que tienen por lo menos un divisor natural distinto de sí mismos y de 1. El número 1, por convenio, no se considera ni primo ni compuesto.
Los números primos menores que 100 son los siguientes: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 y 97.3
La propiedad de ser primo se denomina primalidad. A veces se habla de número primo impar para referirse a cualquier número primo mayor que 2, ya que éste es el único número primo par. A veces se denota el conjunto de todos los números primos por  .
.
 .
.Teorema fundamental de la aritmética
En matemática, y particularmente en la teoría de números, el teorema fundamental de la Aritmética o teorema de factorización única afirma que todo enteropositivo se puede representar de forma única como producto de factores primos. Por ejemplo,
No existe ninguna otra factorización de 6936 y 1200 en números primos. Como la multiplicación es conmutativa, el orden de los factores es irrelevante; por esta razón, usualmente se enuncia el teorema como factorización única salvo en el orden de los factores.
Por definición, un producto vacío tiene por resultado 1, con lo cual el teorema vale también para 1 si se toma como el producto de cero factores.
Número compuesto
Todo número natural no primo, a excepción del 1, se denomina compuesto, es decir, tiene uno o más divisores distintos a 1 y a sí mismo. También se utiliza el término divisible para referirse a estos números.
Los 30 primeros números compuestos son: 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44 y 45.
¿CUANDO UN NUMERO ES DIVISIBLE PARA 2,3,4,5,6,7,9,10 Y 11?
| Un número es divisible por: | Si: | Ejemplo: |
|---|---|---|
| 2 | La última cifra es par (0,2,4,6,8) | 128 es 129 no es |
| 3 | La suma de las cifras es divisible por 3 |
381 (3+8+1=12, y 12÷3 = 4) Sí
217 (2+1+7=10, y 10÷3 = 3 1/3) No
|
| 4 | Las dos últimas cifras son un número divisible por 4 |
1312 es (12÷4=3)
7019 no es |
| 5 | La última cifra es 0 o 5 | 175 es 809 no es |
| 6 | El número es divisible por 2 y 3 | 114 (es par, y 1+1+4=6 y 6÷3 = 2) Sí 308 (es par, pero 3+0+8=11 y 11÷3 = 3 2/3) No |
| 7 | Si doblas la última cifra y la restas del resto del número, y el resultado es:
|
672 (El doble de 2 es 4, 67-4=63, y 63÷7=9) Sí
905 (El doble de 5 es 10, 90-10=80, y 80÷7=11 3/7) No
|
| 8 | Las tres últimas cifras son un número divisible por 8 |
109816 (816÷8=102) Sí
216302 (302÷8=37 3/4) No
|
| 9 | La suma de las cifras es divisible por 9 (Nota: puedes aplicar la regla otra vez a la respuesta si quieres) |
1629 (1+6+2+9=18, y otra vez, 1+8=9) Sí
2013 (2+0+1+3=6) No
|
MAXIMO COMUN DIVISOR
El maximo comun divisor de un conjunto de numeros enteros es el mayor entero positivo , pero es divisor de cada uno de los numeros del conjunto.
87 = 3. 29
105 = 3.5.7
2310 = 2.3.5.7.11
m.c.d = (87,105,2310) = 3
APLICACION
Un vendedor dispone de 24 , 36 y 48 umidades de 3 articulos diferentes , respectivamente . necesita elaborar paquetes por cada articulo , de tal forma que el numero de unidades de todos los paquetes sea el mismo y el mas grande posible . cuantas unidades debe tener cada paquete .
24 36 48 | 2
12 19 24 | 2
6 9 12 | 2
3 9 6 | 2
3 9 3 | 3 m.c d { 2.2.3 } = 12
1 3 3 | 3
MINIMO COMUN MULTIPLO
El minimo comun multiplo de un conjunto de numeros enteros es el menor entero positivo que es el multiplo de cada uno de los numeros dados .
APLICACIONES
Un fabricante tiene 3 productos en su inventario , los cuales se revisan periodicamente cada 2 , 6 y 10 semanas , respectivamente. el fabricante necesita calcular cual sera el minimo tiempo que debe transcurrir en semanas para que la revision de los 3 productos coincidan .
2 6 10 | 2
1 3 5 | 3
1 1 5 | 5
1 m.c.m = 2.3.5 = 30
Un ebanista ahorrador quiere cortar una plancha de madera de 256 cm de largo y 96 cm de ancho , encuadros los mas grandes posibles . Cual debe ser la longitud del lado de cada cuadro ?
256 96 | 2
128 48 | 2
64 24 | 2
32 12 | 2
16 6 | 2
8 3 | 2
4 3 | 2
2 3 | 2
1 3 | 3
1 2.2.2.2.2 = 32
R = La longitud es 32 cm .
una cita en sevilla.
Un viajero va a sevilla cada 18 dias otro va a sevilla cada 15 dias y un tercer va a sevilla cada 8 dias .
hoy 10 de junio han coincidido en sevilla los 3 viajeros dentro de cuantos dias como minimo volveran a coincidir en sevilla .
18 15 8 | 2
9 15 4 | 2
9 15 2 | 2
9 15 1 | 3
3 5 | 3
1 5 | 5
1 m.c.m 0= 2.2.2.3.3.5 = 360
R = 5 de junio del 2016.
Números pares e impares
En matemática, un número par es un número entero que se puede escribir de la forma: 2k (es decir, divisible de manera entera entre 2), donde k es un entero (los números pares son los múltiplos del número 2). Los números enteros que no son pares, se llaman números impares (o nones), y se pueden escribir como 2k+1.1
Los números pares son:
y los impares:
La paridad de un número entero se refiere a su atributo de ser par o impar.2 Comparativamente, dos números son «de la misma paridad» si al dividirlos entre 2, el resto es el mismo, por ejemplo: "2" y "4", o "3" y "7"; son «de la misma paridad». Por el contrario los números "23" y "44" son «de distinta paridad».
JERARQUIA DE OPERACIONES
12 + 6 : 3 - 5 x 2
12 + 2 - 10
12 + ( -8 )
12 - 8 =
4 R//
Combinación de sumas, restas, productos, divisiones y potencias.
23 + 10 : 2 + 5 · 3 + 4 - 5 · 2 - 8 + 4 · 22 - 16 : 4 =
Realizamos en primer lugar las potencias por tener mayor prioridad.
= 8 + 10 : 2 + 5 · 3 + 4 - 5 · 2 - 8 + 4 · 4 - 16 : 4 =
Seguimos con los productos y cocientes.
= 8 + 5 + 15 + 4 - 10 - 8 + 16 - 4 =
Efectuamos las sumas y restas.
= 26
Operaciones combinadas con paréntesis y corchetes
[15 - (23 - 10 : 2 )] · [5 + (3 ·2 - 4 )] - 3 + (8 - 2 · 3 ) =
Primero operamos con las potencias, productos y cocientes de los paréntesis.
= [15 - (8 - 5 )] · [5 + (6 - 4 )] - 3 + (8 - 6 ) =
Realizamos las sumas y restas de los paréntesis.
= [15 -3 ] · [5 + 2 ] - 3 + 2=
Operamos en los paréntesis.
= 12 · 7 - 3 + 2
Multiplicamos.
= 84 - 3 + 2=
Restamos y sumamos.
= 83
Definición de decimal
La palabra "Decimal" quiere decir "basado en 10" (de la palabra latina décima: una parte de diez).
A veces decimos "decimal" cuando hablamos de nuestro sistema de números, pero un "número decimal" normalmente tiene un punto decimal.
EJEMPLOS
0,25 1,445 0,7892 00= DECIMAL FINITOS
0,66 0,77 0= DECIMAL PERIODICO INFINITO
 DECINALES MIXTOS
DECINALES MIXTOS
CONVERSION EN FRACCIONES
La palabra "Decimal" quiere decir "basado en 10" (de la palabra latina décima: una parte de diez).
A veces decimos "decimal" cuando hablamos de nuestro sistema de números, pero un "número decimal" normalmente tiene un punto decimal.
EJEMPLOS
0,25 1,445 0,7892 00= DECIMAL FINITOS
0,66 0,77 0= DECIMAL PERIODICO INFINITO
 DECINALES MIXTOS DECINALES MIXTOS
CONVERSION EN FRACCIONES
|
Ejemplo 1: Expresar 0,75 como fracción
Paso 1: Escribe:
Paso 2: Multiplica el numero de abajo y el de arriba por 100 (porque hay 2 dígitos luego de la coma):
(¿Ves como el número de arriba se convierte
en un entero?)
Paso 3: Simplifica la fracción:
| |||||||||||||||||||||||||||||||||||||||||
Respuesta = 3/4
Nota: ¡75/100 se llama una fracción decimal y 3/4 es llamada una fracción común !
Nota: ¡75/100 se llama una fracción decimal y 3/4 es llamada una fracción común !
|
Ejemplo 2: Expresa 0,625 como una fracción
Paso 1: escribe:
Paso 2: multiplica el número de arriba y el de abajo por 1,000 (había 3 dígitos luego de la coma así que es 10×10×10=1,000)
Paso 3: simplifica la fracción (me llevó dos pasos aquí):
| |||||||||||||||||||||||||||||||||||||
Respuesta = 5/8
PERIODICO PURO

CUANDO ES NO PERIODICO
Ejemplo 1: 0,2555...
0,2555 = (25 -2)/90 = 23/90
Asi, 0,2555... es igual a 23/90.
Ejemplo 2: 7,67151515...
7,671515... = (7615 -767)/9900 = 6848/9900 = 1712/2475
Finalmente 7,671515... es igual a 1712/2475
CONSULTA SOBRE RAZONES Y PROPORCIONES
Razones y Proporciones
Llamamos razón al cociente indicado de dos números:
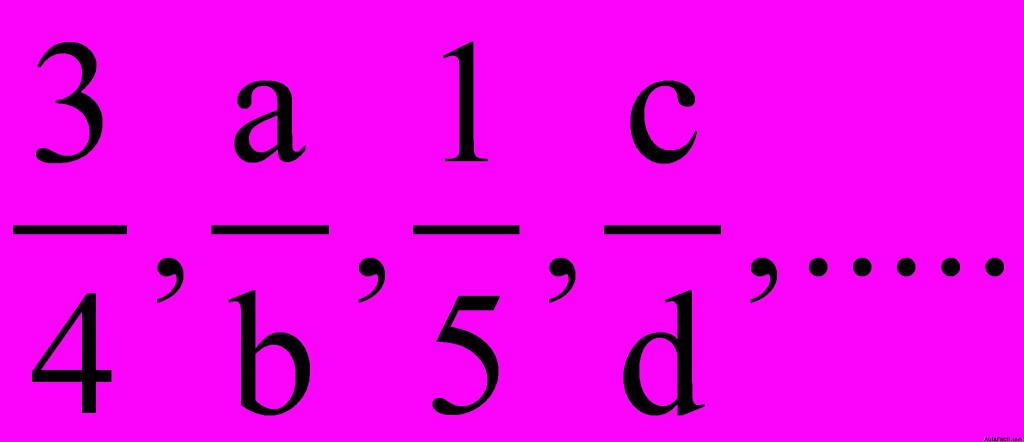 son razones que como ves, se tratan de divisiones que están indicadas, sin calcular su resultado.
son razones que como ves, se tratan de divisiones que están indicadas, sin calcular su resultado.
Llamamos proporción a la igualdad de dos razones:
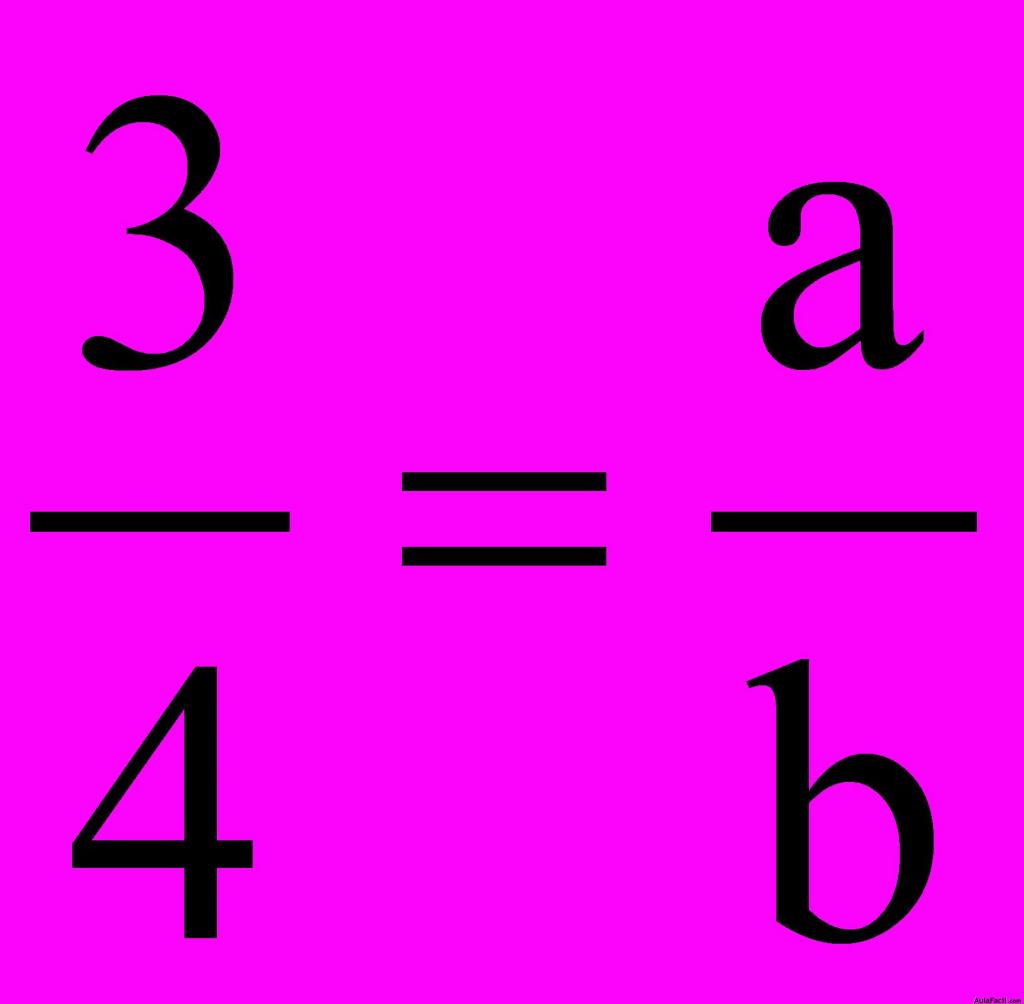 Es una proporción porque tenemos igualadas dos razones;
Es una proporción porque tenemos igualadas dos razones; 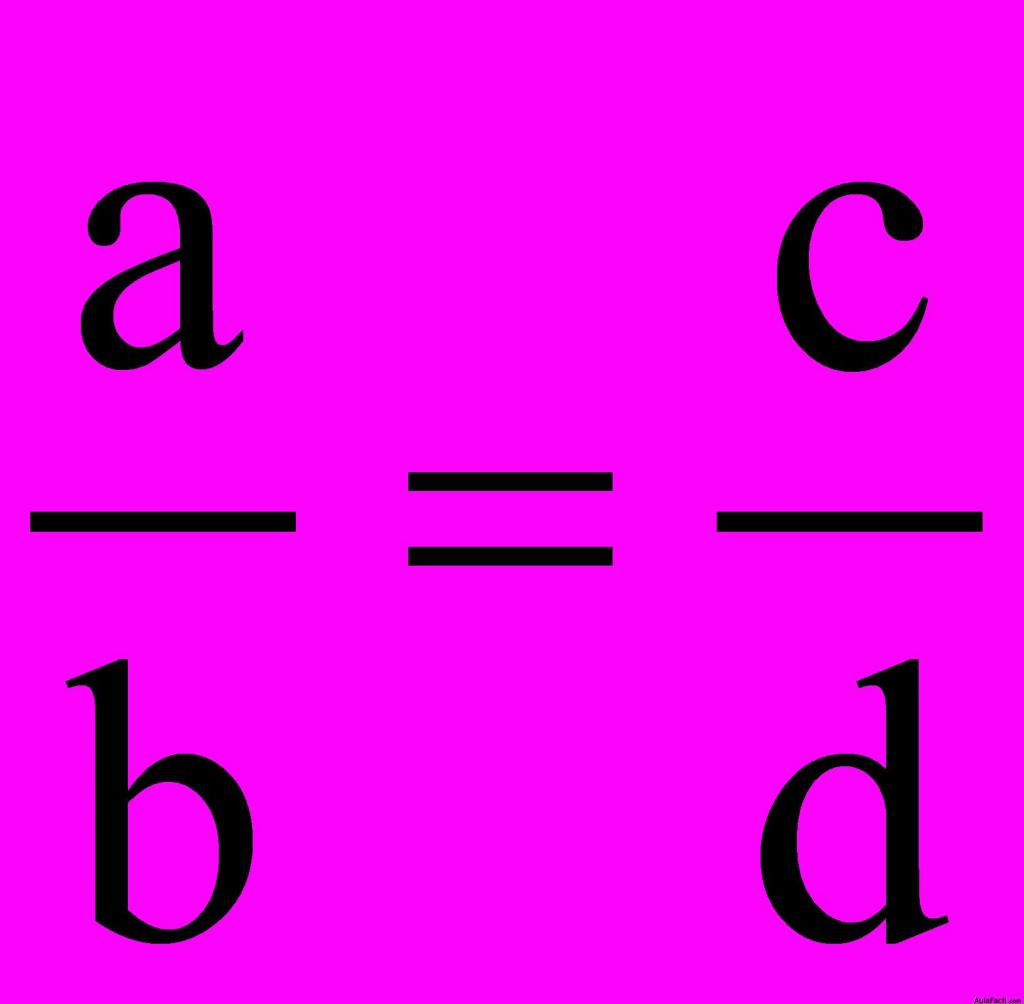 es otra proporción porque tenemos la igualdad de dos razones.
es otra proporción porque tenemos la igualdad de dos razones.
La proporción: 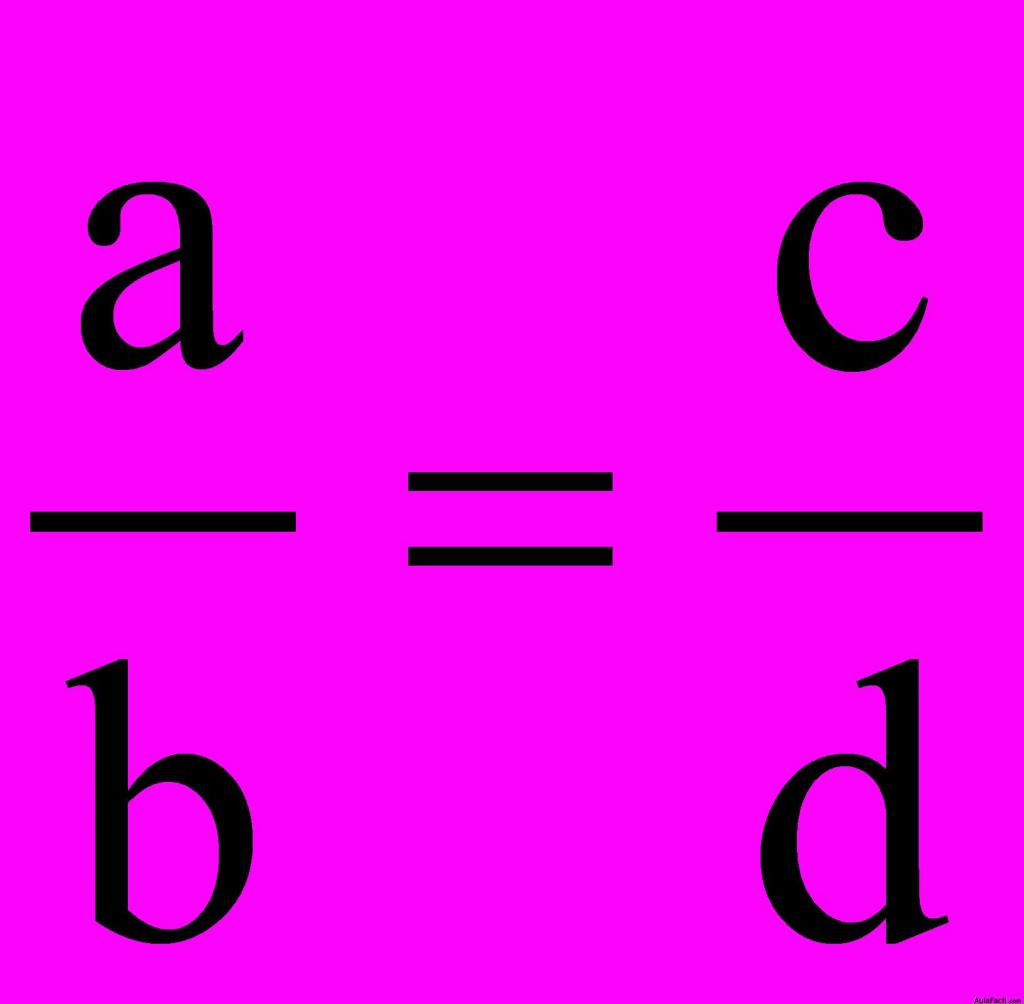 se lee: ‘a’ ES‘b’ COMO’c’ES a ‘d’.
se lee: ‘a’ ES‘b’ COMO’c’ES a ‘d’.
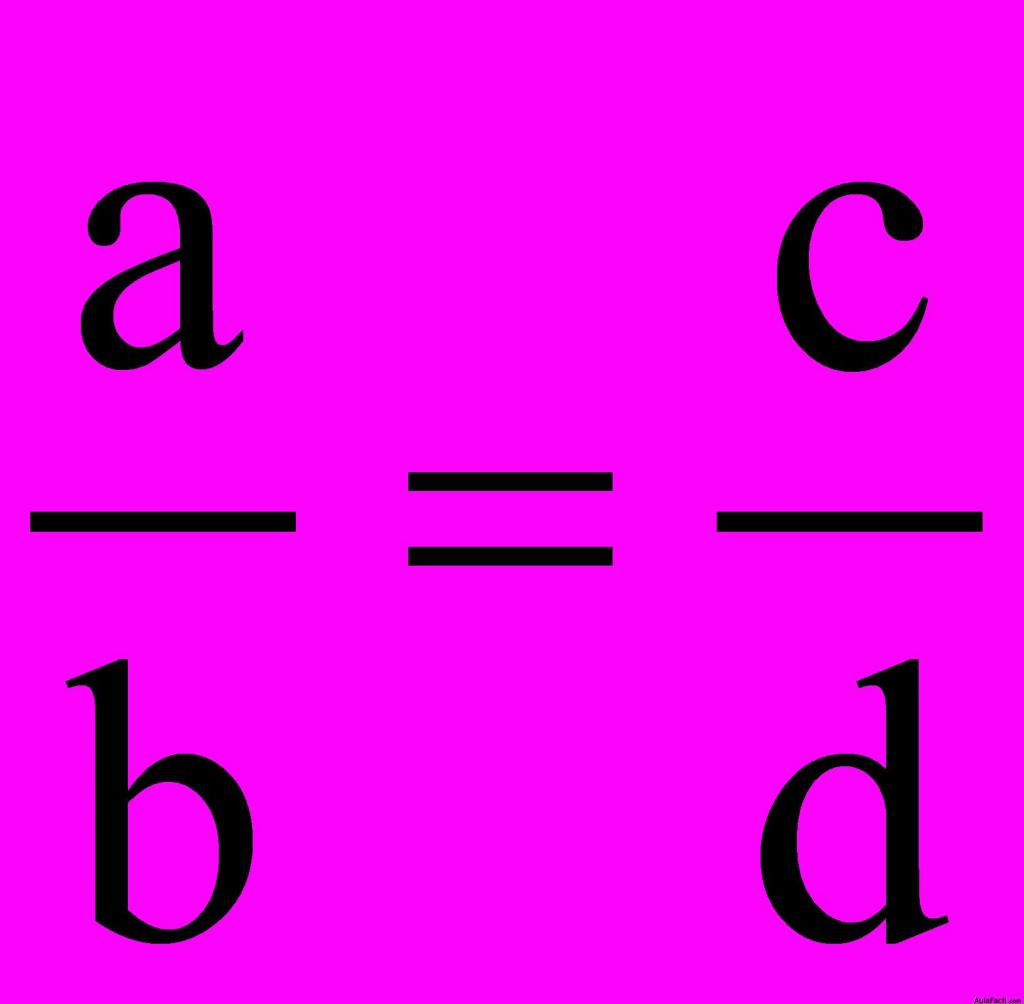 se lee: ‘a’ ES‘b’ COMO’c’ES a ‘d’.
se lee: ‘a’ ES‘b’ COMO’c’ES a ‘d’.
En la vida de cada día vemos que muchas cosas son proporcionales:
1) Velocidad de un automóvil con el consumo de gasolina (a más velocidad, mayor consumo de combustible).
2) Valor de un saco de patatas con los kilos que pesa (a más kilos mayor importe a pagar).
3) Precio de un billete de tren con la distancia a recorrer (cuanto más lejos vaya, más dinero pagaré por el billete).
Existen muchos otros ejemplos….
2) Valor de un saco de patatas con los kilos que pesa (a más kilos mayor importe a pagar).
3) Precio de un billete de tren con la distancia a recorrer (cuanto más lejos vaya, más dinero pagaré por el billete).
Existen muchos otros ejemplos….
Los componentes de una proporción se llaman: Extremos y medios.
Los extremos, como su nombre indican son el primero y último términos de la proporción.
Los medios, los que están entre los dos anteriores; segundo y tercerotérminos.
En la proporción: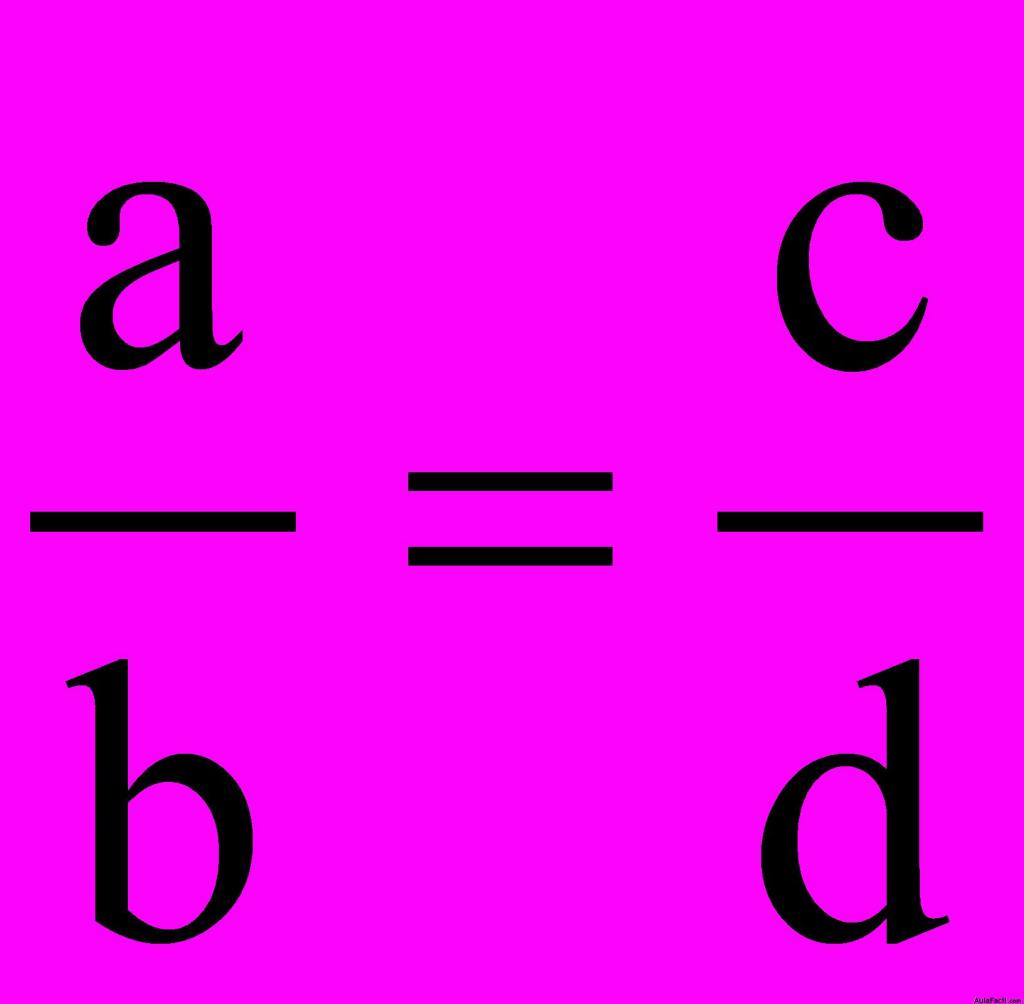 , a y d son los extremos, b y c los
, a y d son los extremos, b y c los
medios.
Los extremos, como su nombre indican son el primero y último términos de la proporción.
Los medios, los que están entre los dos anteriores; segundo y tercerotérminos.
En la proporción:
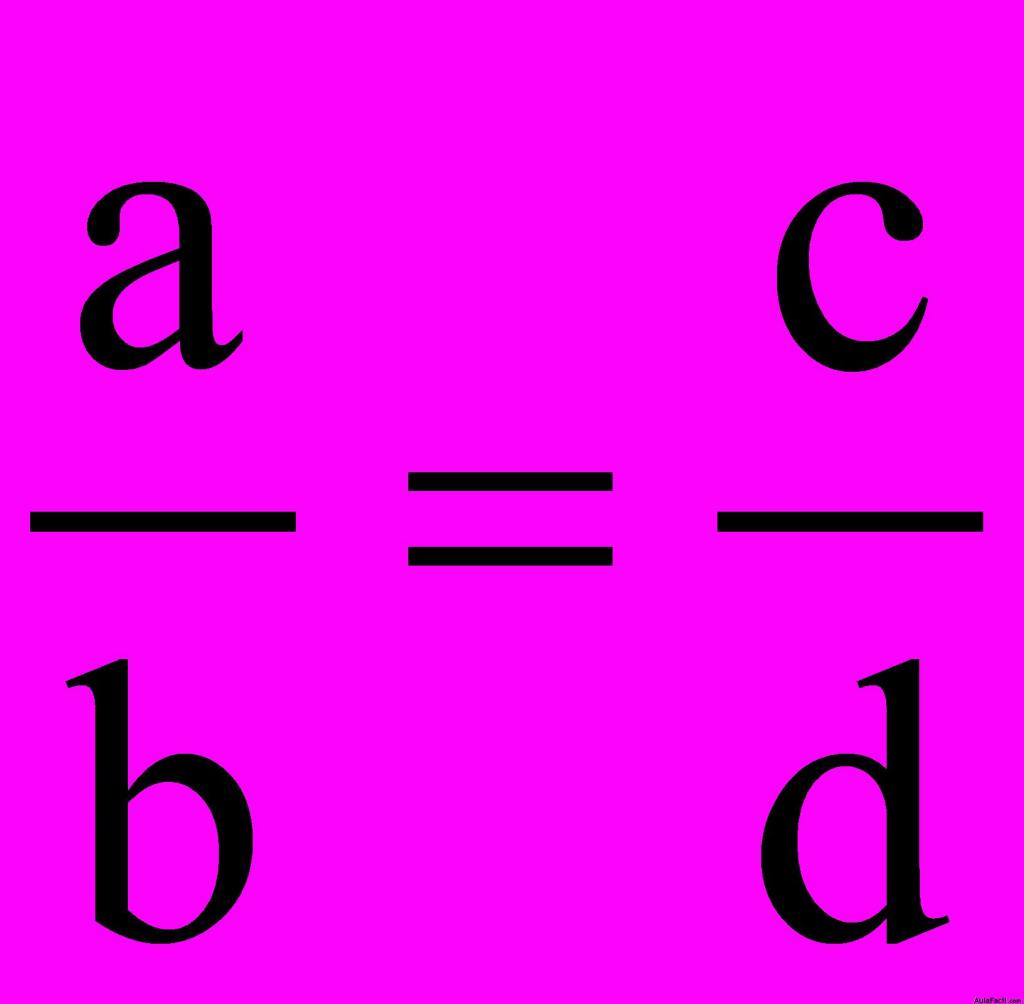 , a y d son los extremos, b y c los
, a y d son los extremos, b y c losmedios.
1) En toda proporción, el producto de los extremos es igual al producto de los medios.
2) El cociente de las dos fracciones de una proporción siempre son iguales.(Porque las fracciones son equivalentes)
2) El cociente de las dos fracciones de una proporción siempre son iguales.(Porque las fracciones son equivalentes)
Veamos la siguiente proporción: 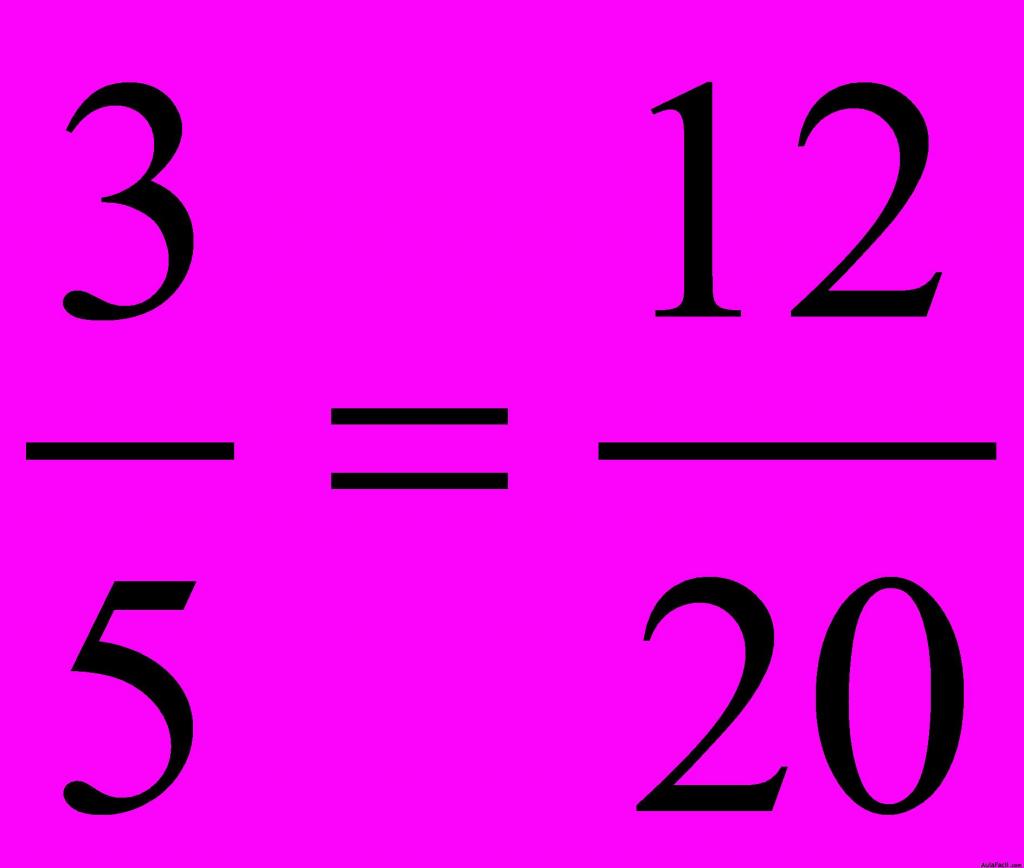
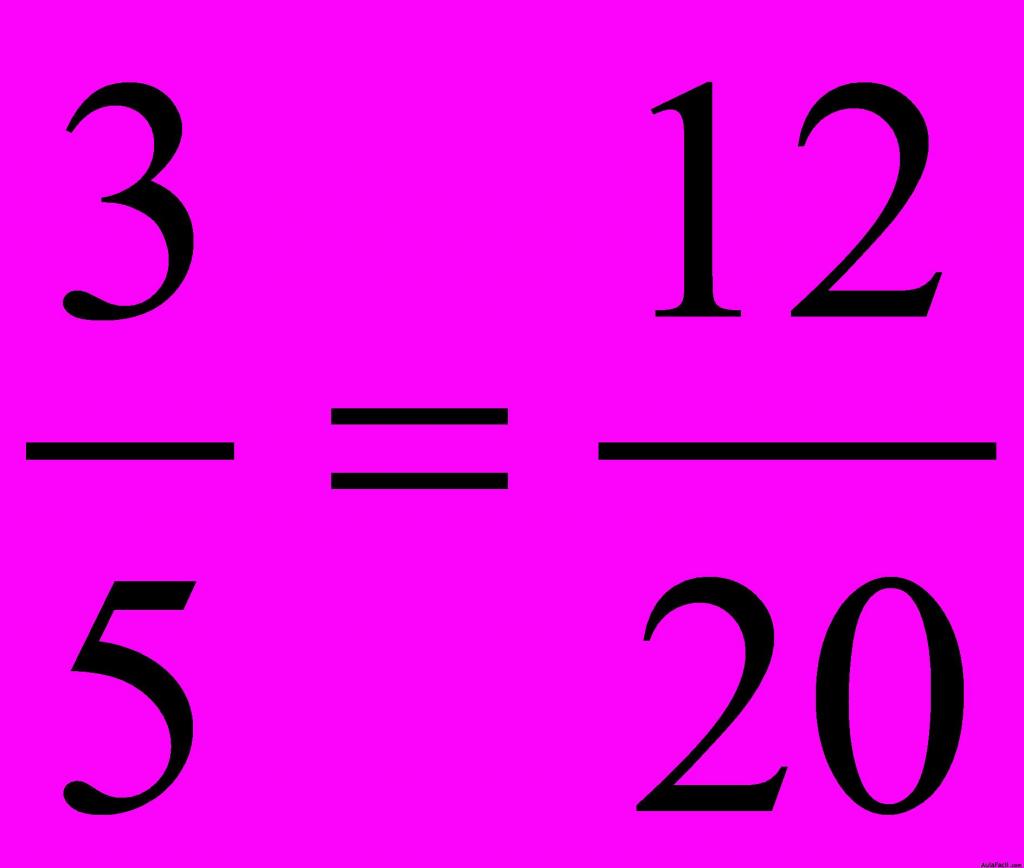
1) El producto de los extremos es: 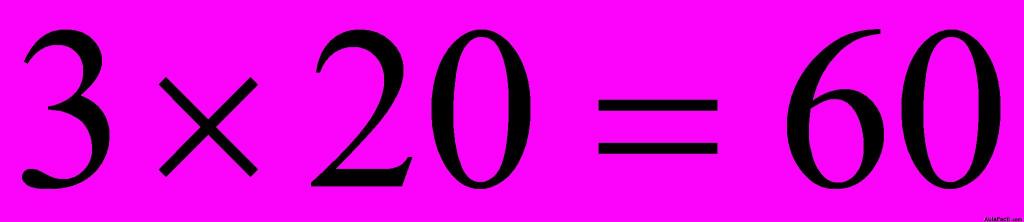
2) El producto de los medios es: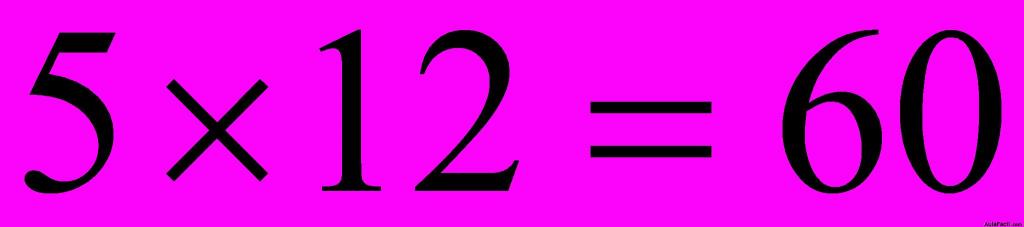
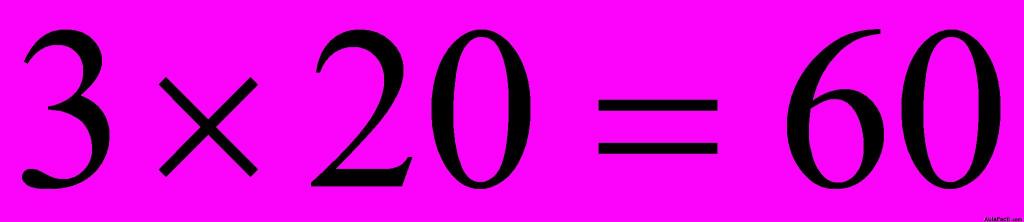
2) El producto de los medios es:
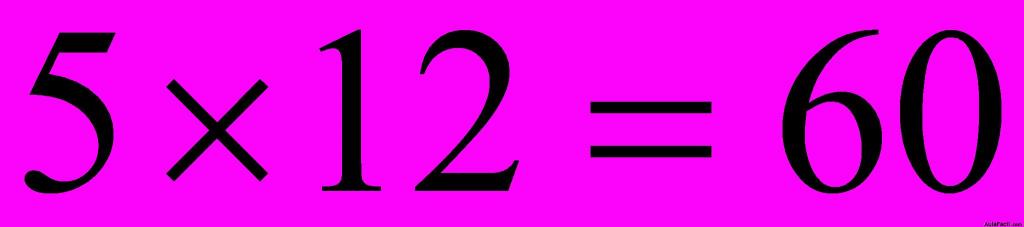
El cociente de 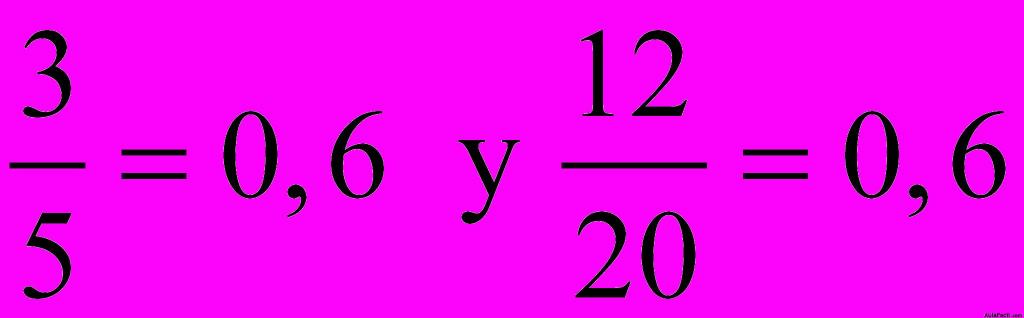 son iguales.
son iguales.
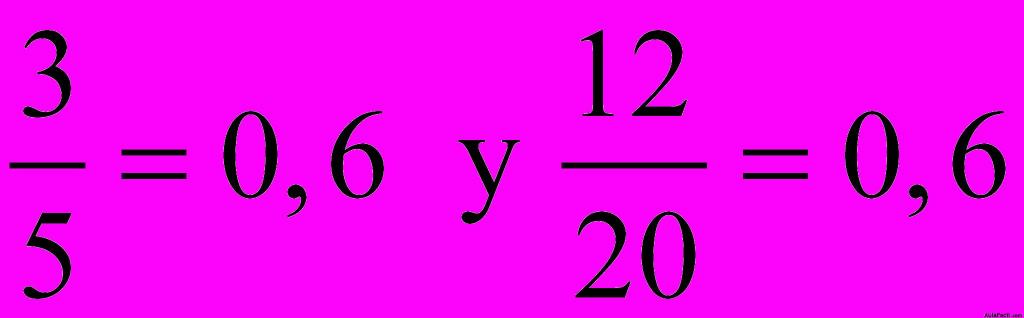 son iguales.
son iguales.
Al cociente de las fracciones de una proporción se llama constante de proporcionalidad (muy útil para resolver problemas que tratan de repartos proporcionales).
6.36 ¿Crees que 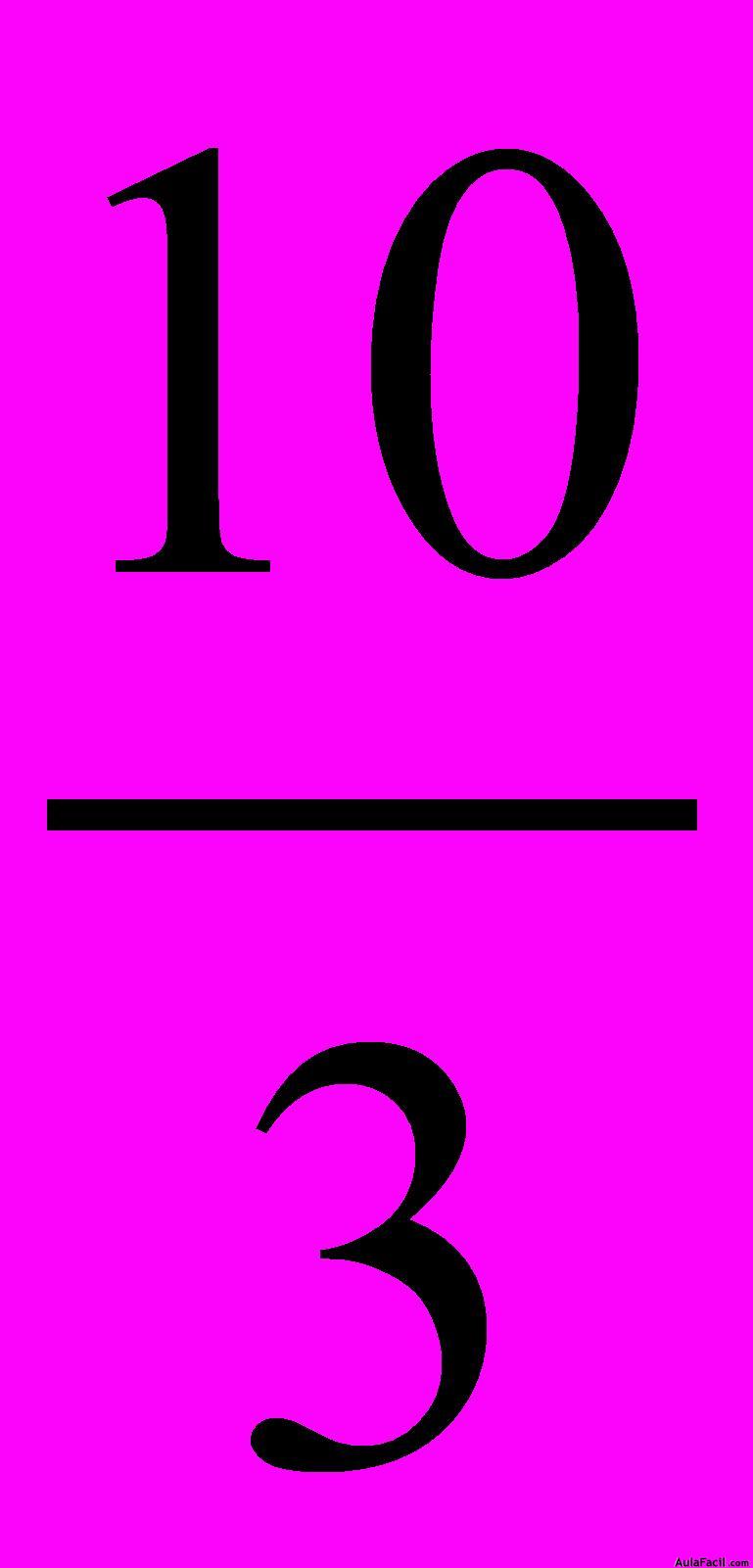 y
y 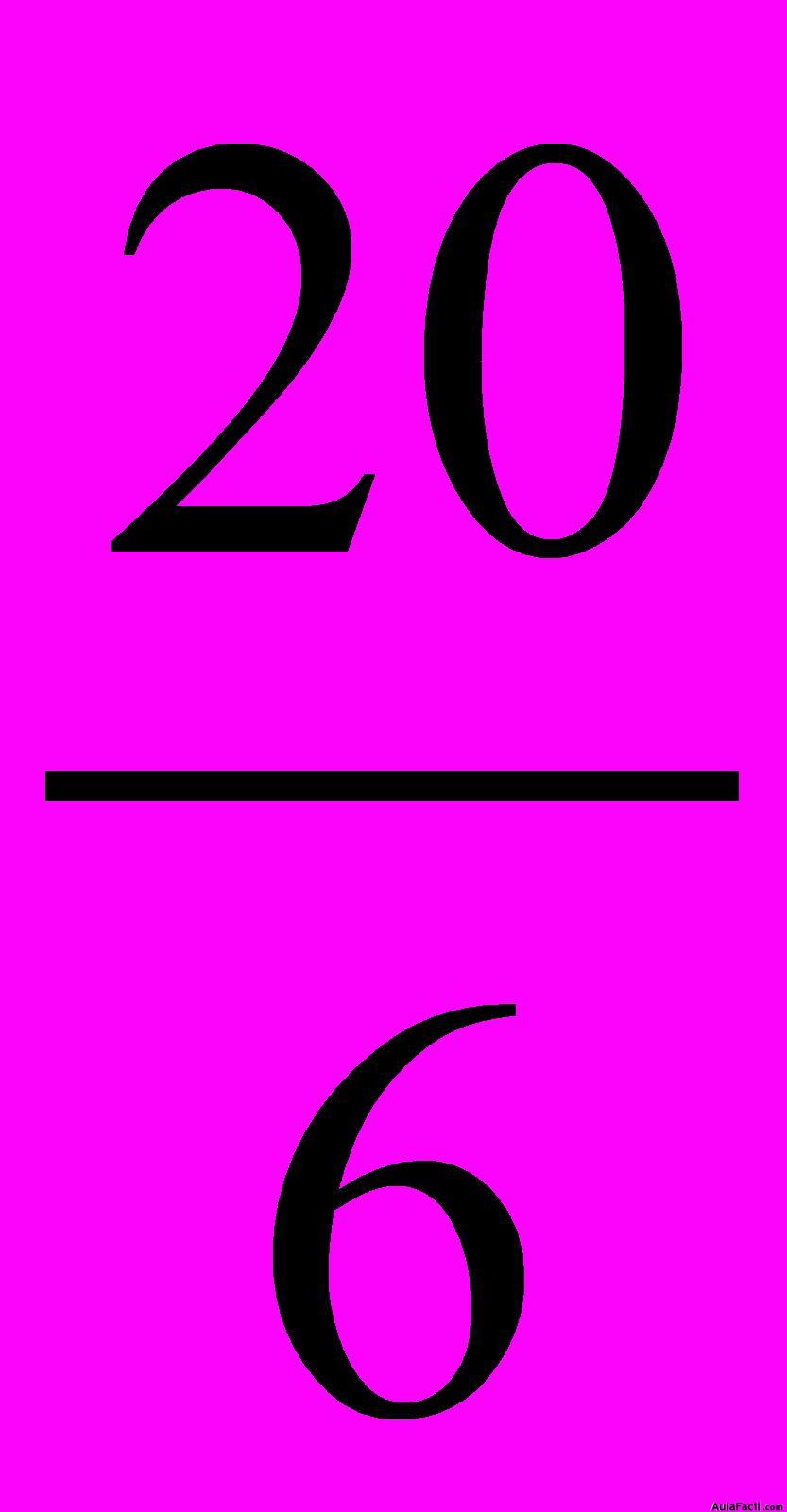 forman una proporción?
forman una proporción?
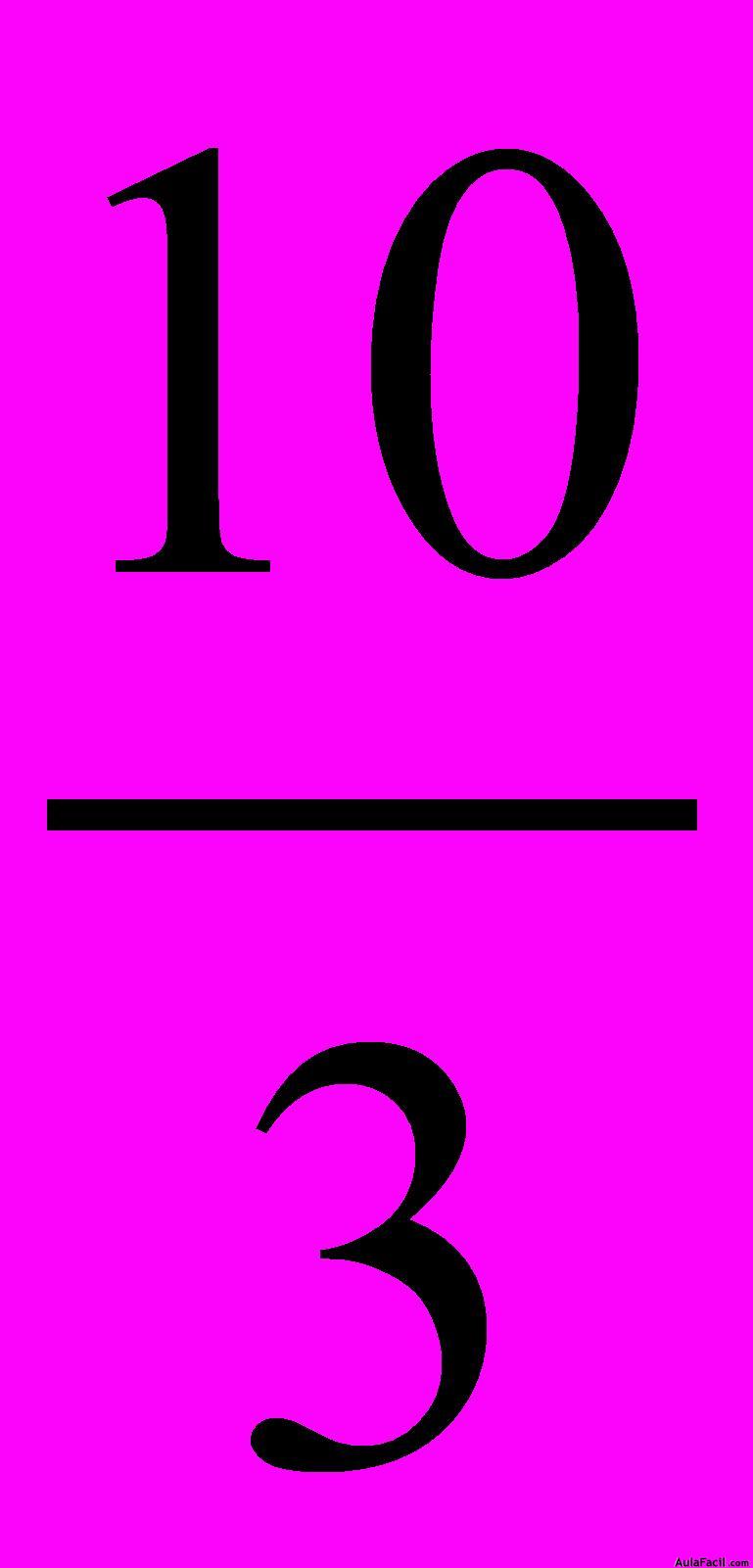 y
y 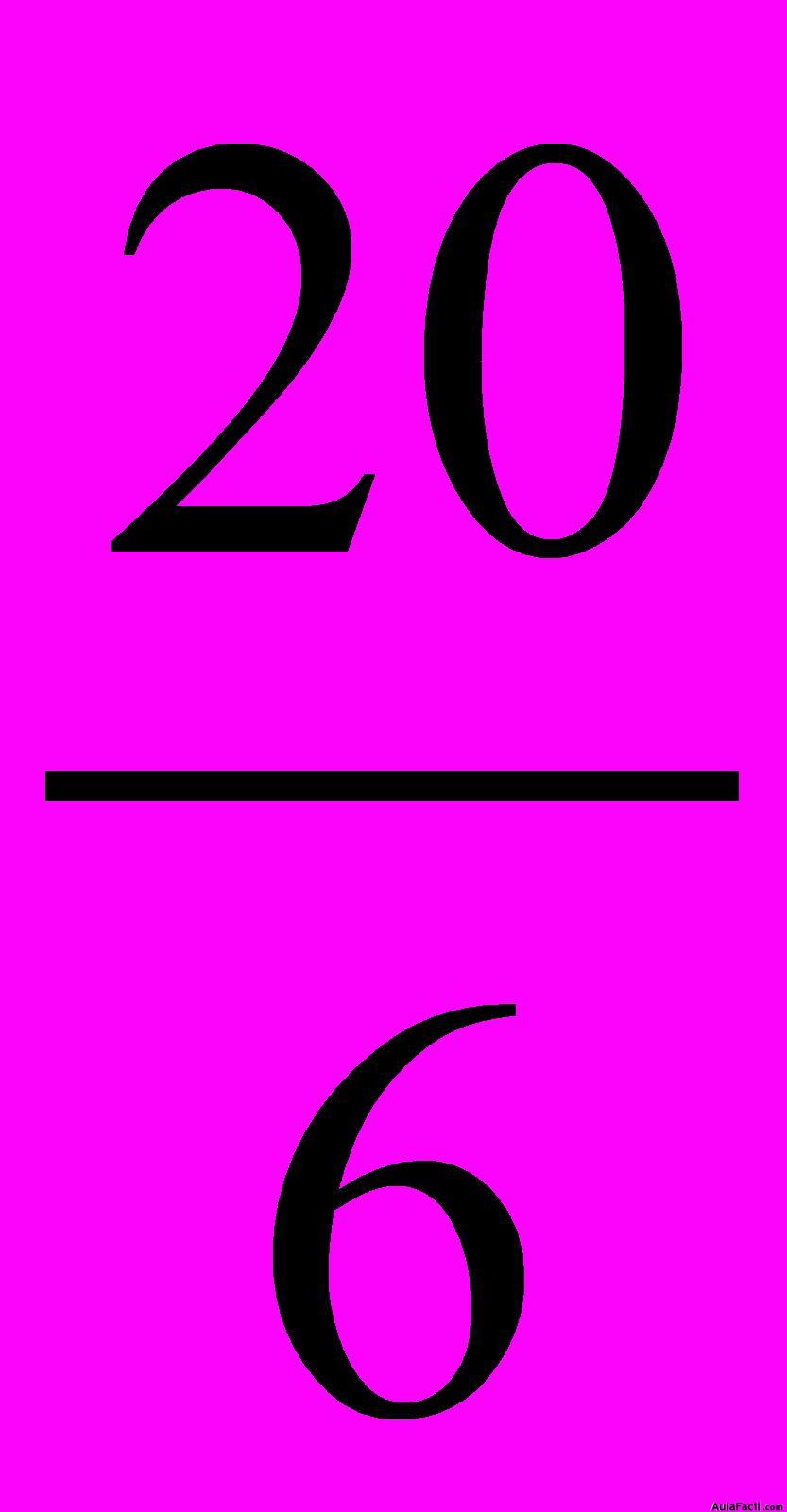 forman una proporción?
forman una proporción?
Respuesta: Sí porque el producto de extremos es igual al producto de medios y porque se trata de fracciones equivalentes.
6.37 ¿Cuál es la constante de proporcionalidad en 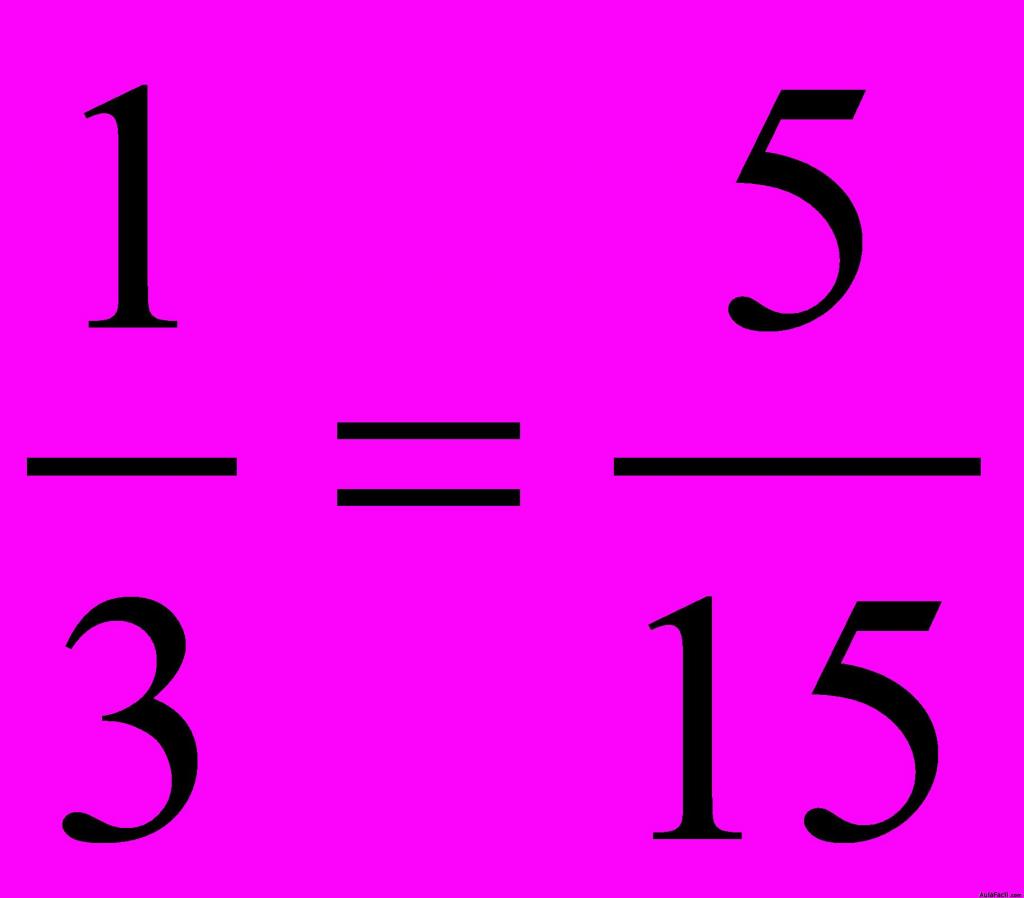 ?
?
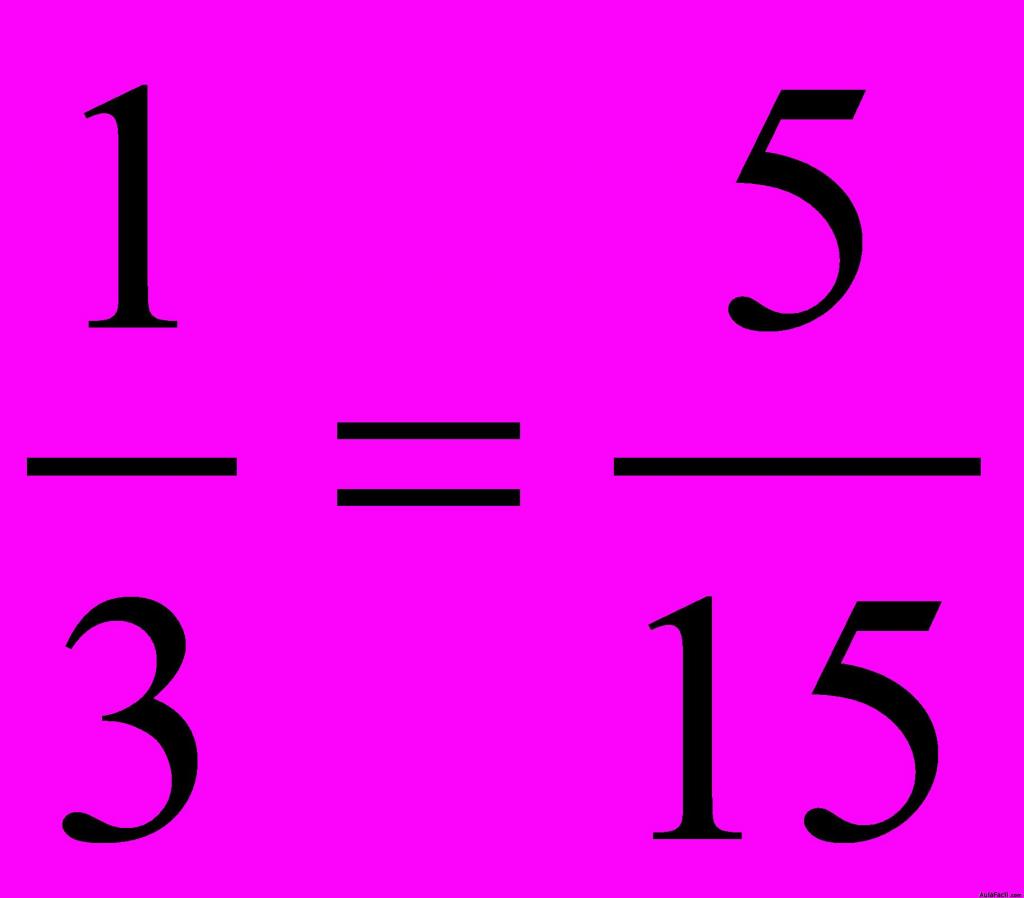 ?
?
Respuesta: 
PROPORCIONES Y REGLA DE TRES:
Los problemas que hicimos utilizando la regla de tres, podemos resolverlos haciendo uso de las proporciones.
Proporcionalidad directa (regla de tres directa):
Proporcionalidad directa (regla de tres directa):
En una proporción en la que nos dan el valor de 3 datos, podemos calcular el cuarto de un modo muy simple. Veamos en un ejemplo:
6.38 Un vehículo recorre 300 kilómetros con 25 litros de gasolina. ¿Cuántos kilómetros podría recorrer con 200 litros?
Respuesta:
Solución:
Por regla de tres escribimos los datos conocidos:
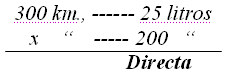
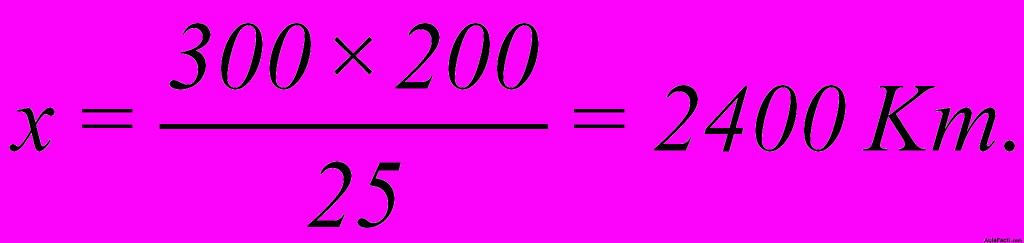
Si la regla de tres es directa, cada pareja de datos, debidamente ordenados, los podemos escribir en forma de dos razones:
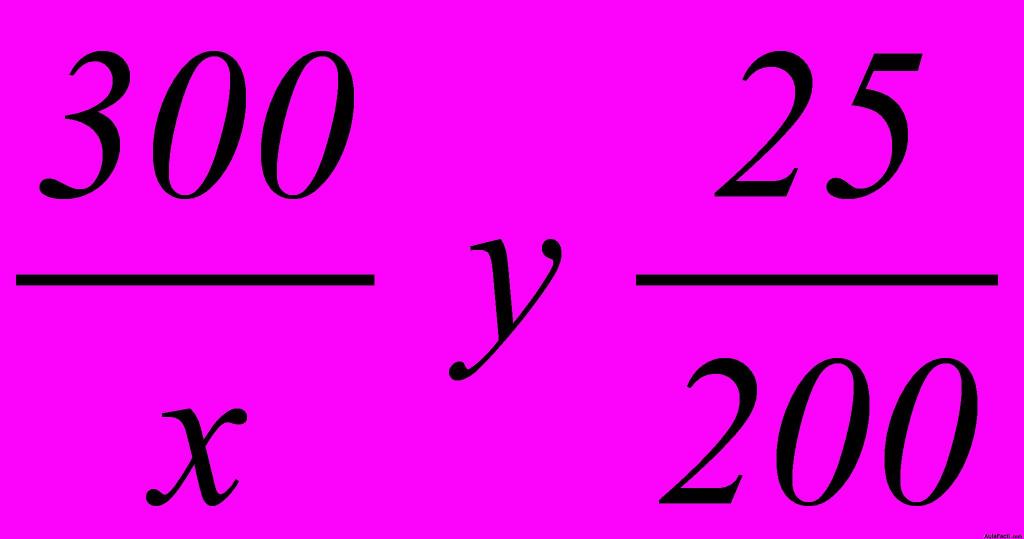 , como ves, en el mismo orden tal como los habíamos escrito en la regla de tres.
, como ves, en el mismo orden tal como los habíamos escrito en la regla de tres.
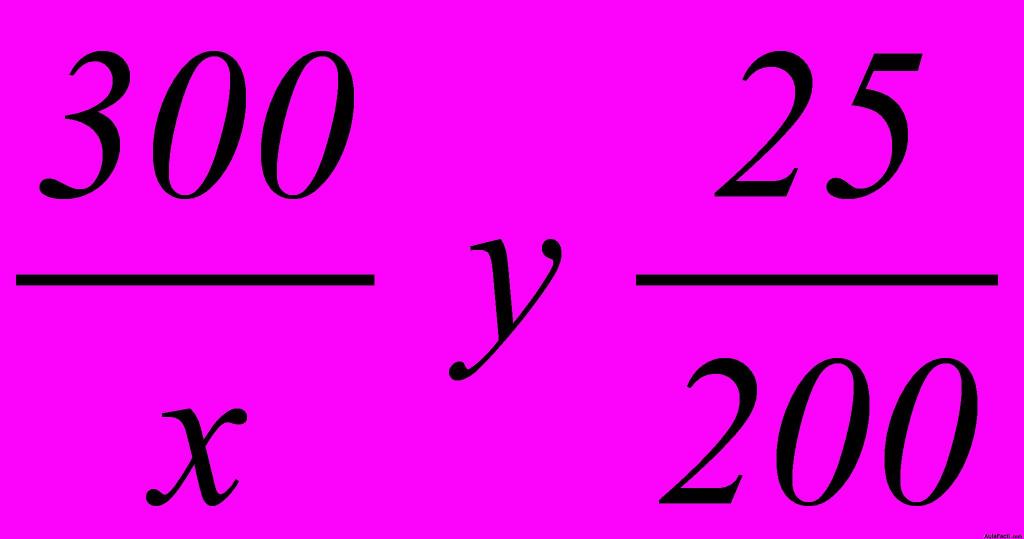 , como ves, en el mismo orden tal como los habíamos escrito en la regla de tres.
, como ves, en el mismo orden tal como los habíamos escrito en la regla de tres.
Colocamos estas dos razones en forma de proporción: 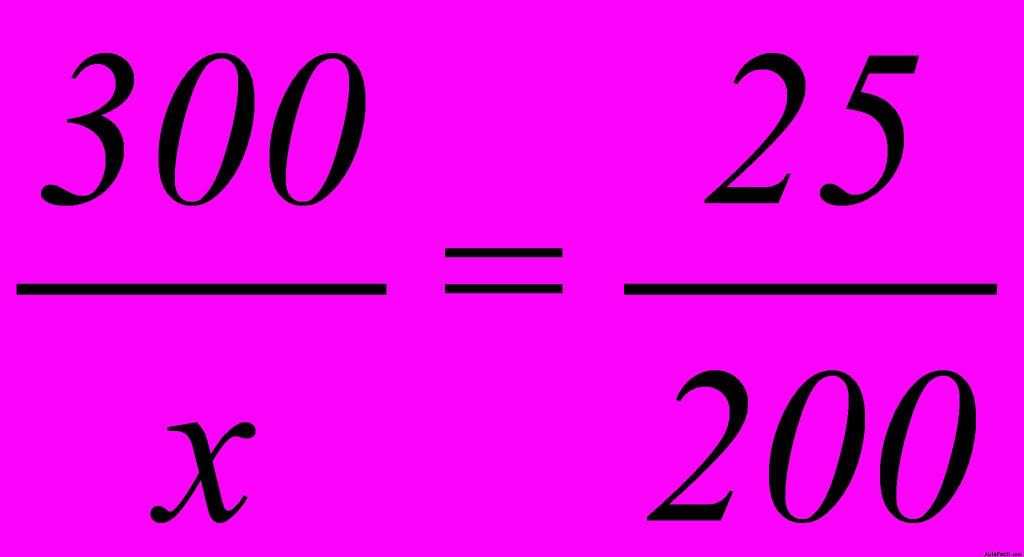
Sabemos que en toda proporción el producto de extremos es igual al producto de medios:
300 200 = 25
200 = 25 x
x
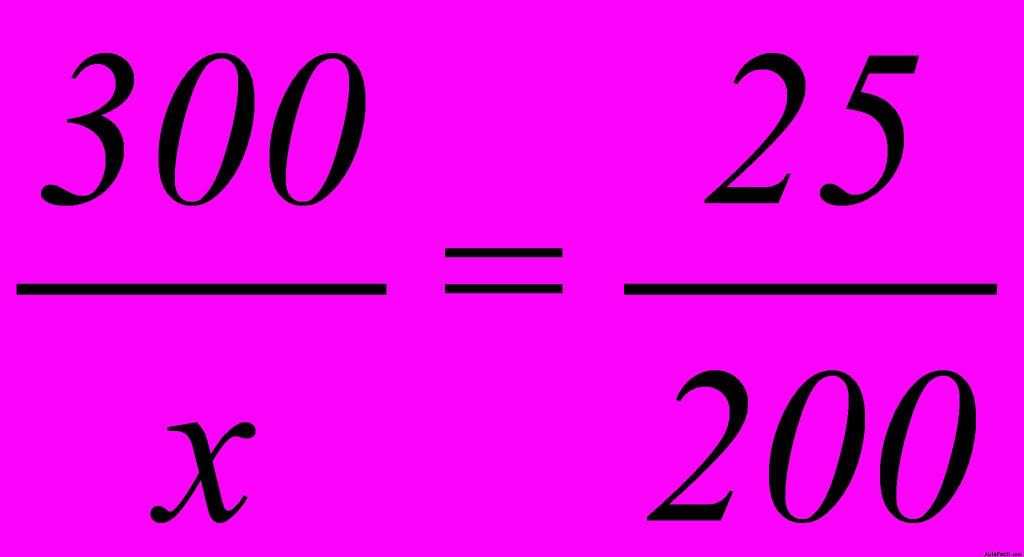
Sabemos que en toda proporción el producto de extremos es igual al producto de medios:
300
Para calcular el valor de x tenemos que pasar el número (25) que lo multiplica al otro lado del signo =, es decir, donde se encuentran 300 200 pero cuando un dato pasa al otro lado del signo igual lo hace con el signo contrario al que tenía: si le sumaba a ‘x’ pasa restando, si estaba restando pasa sumando, si estaba multiplicando, pasa dividiendo y se le estaba dividiendo pasa multiplicando.
200 pero cuando un dato pasa al otro lado del signo igual lo hace con el signo contrario al que tenía: si le sumaba a ‘x’ pasa restando, si estaba restando pasa sumando, si estaba multiplicando, pasa dividiendo y se le estaba dividiendo pasa multiplicando.
En el caso actual, 25 multiplica a ‘x’, luego, pasará dividiendo:
En el caso actual, 25 multiplica a ‘x’, luego, pasará dividiendo:
6.39 Una rueda da 1000 vueltas en 4 minutos ¿Cuántas vueltas dará en 1 hora?. Resuelve utilizando las proporciones:
Respuesta: 15000 vueltas.
Solución:Directamente establecemos la proporción: 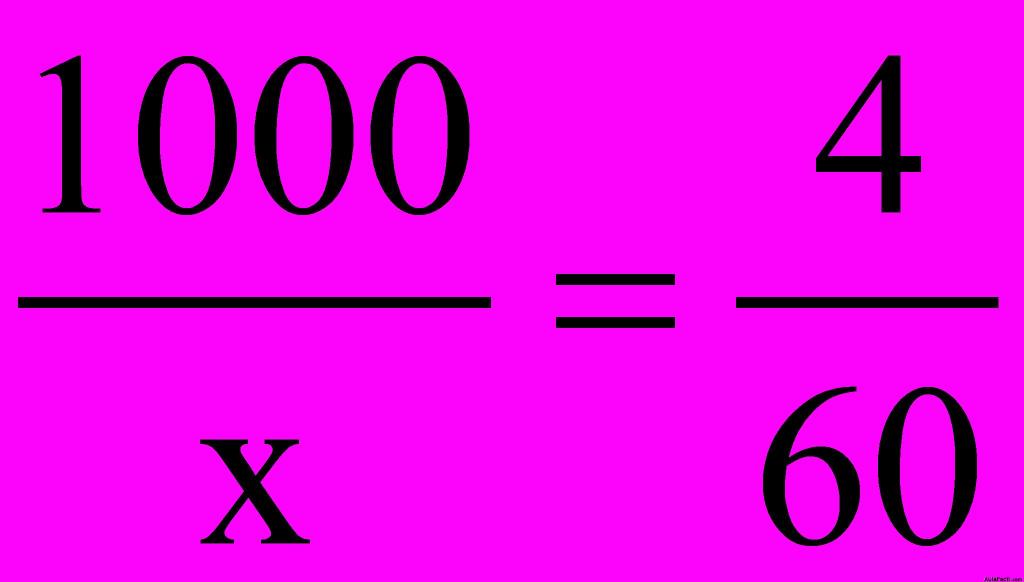
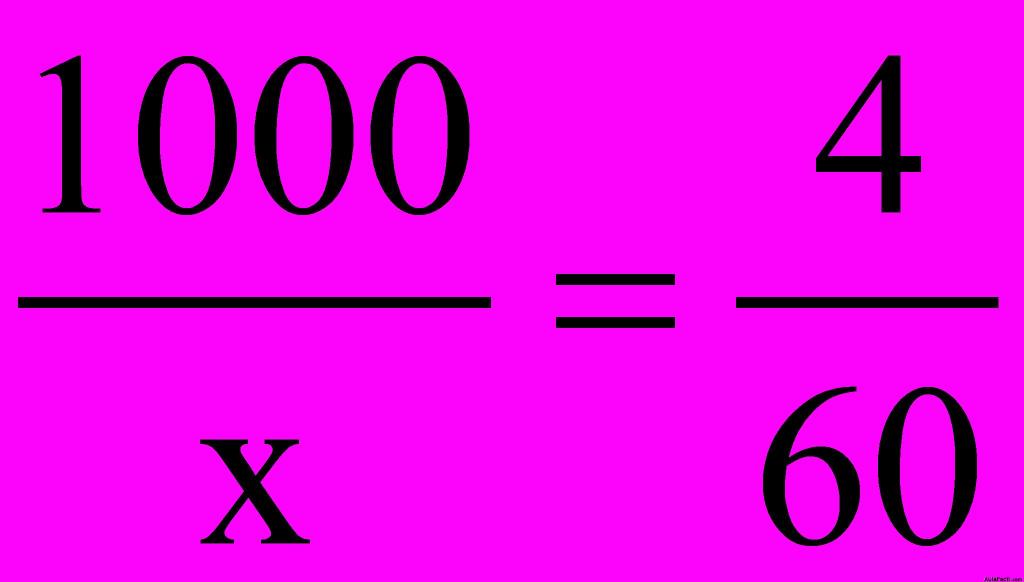
6.40 Con 30 € puedo comprar 2 camisas ¿cuántas podré comprar con 180 €? Resolverlo haciendo uso de las proporciones.
Respuesta: 12 camisas
Solución:
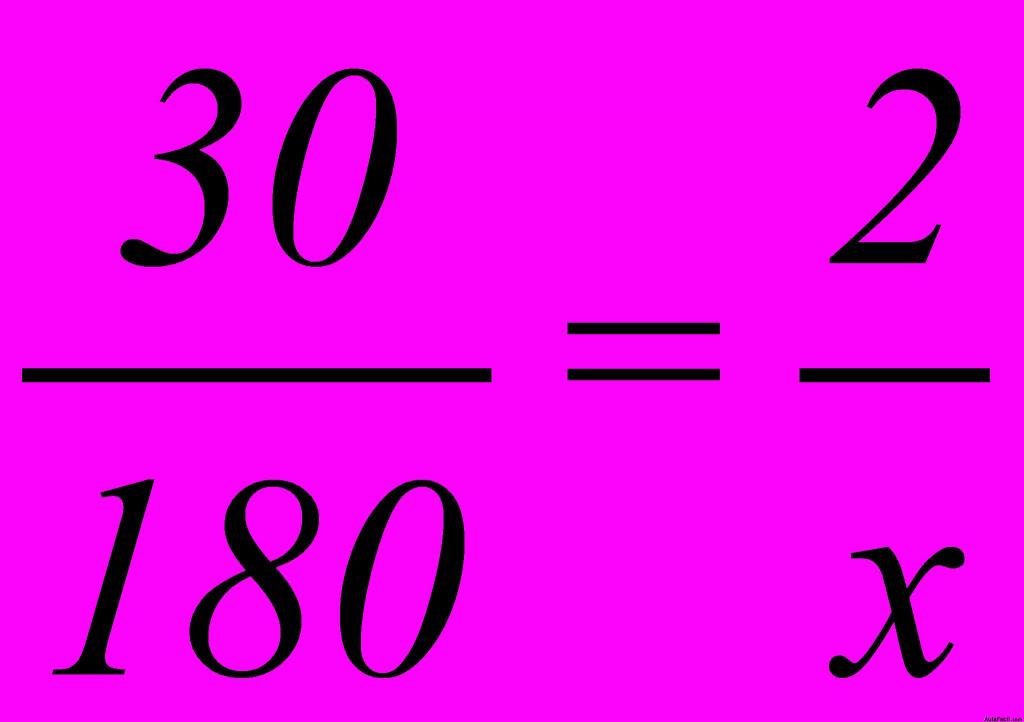
6.41 Para construir 5 casas se han utilizado 22000 kilos de cemento. ¿Cuántas casas podremos hacer con 132000 kilos?
Respuesta: 30 casas
video del tema razones y proporciones
Si 2 agricultores tardan 10 días en arar un campo, ¿cuánto tardarán 5 agricultores en realizar el mismo trabajo?
Se trata claramente de un ejemplo de proporción inversa, puesto que a más agricultores trabajando menos tiempo se tardará en arar el mismo campo.
Para resolverlo se aplica la regla de tres como se ha enseñado:
Y se resuelve:
Es decir, mientras que dos agricultores tardan 10 días, con la ayuda de otros 3 compañeros consiguen hacer el mismo trabajo en tan solo 4 días.
Si el kilo de cerezas va a 4,5 €, ¿cuánto costará comprar medio kilo?
Tenemos una proporcionalidad directa puesto que a menos kilos que compremos más barato nos costará.
Tenemos la relación de proporcionalidad:
Aplicando la regla de tres tenemos:
Es decir, medio kilo de cerezas costarán la mitad que un kilo.
INTERVALOS
DEFINICION = Se llama intervalo al conjunto de numeros reales comprendidas entre otra dos dadas= A y B se llaman extremos de los intervalos.
TIPOS DE INTERVALOS :
Es aquel intervalo en que ninguno de los extremos pertenecen al conjunto que él representa
INTERVALO CERRADO
Es aquel intervalo en que ambos extremos pertenecen al conjunto que él representa
INTERVALO SEMI-CERRADO (SEMI-ABIERTO)
Es cerrado por la derecha y abierto por la izquierda, e incorpora solo al límites "b" entre sus componentes.
INTERVALOS INFINITOS
En este tipo de intervalos se conoce el límite izquierdo pero no el derecho. Para este tipo de intervalos se pueden dar dos situaciones, que el intervalo sea abierto ó el intervalo sea cerrado en la izquierda, en cuyo caso se representan:
INFINITO NEGATIVO
En este tipo de intervalos se conoce el límite derecho pero no el izquierdo. Para este tipo de intervalos se pueden dar dos situaciones, que el intervalo sea abierto ó el intervalo sea cerrado en la derecha, en cuyo caso se representan:
IDENTIDAD O IGUALDAD ABSOLUTA = es un enunciado que compara 2 expresiones matematicas con el
simbolo igual ( = ) y es verdadera para todos los valores de las variables del conjunto referencial que corresponda
Identidades notables[editar]
Artículo principal: Productos notables
Algunas identidades algebraicas se denominan «notables» y facilitan los cálculos o la factorización de expresiones polinómicas.
Por ejemplo el producto notable
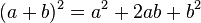 , que es cierto sean cuales sean los elementos , que es cierto sean cuales sean los elementos  y y  de un anillo conmutativo. de un anillo conmutativo.Identidades aritméticas[editar]
Algunas de las identidades aritméticas más notables son la suma de términos de una progresión aritmética, entre la que se encuentra la suma de los n primerosnúmeros naturales (desde el 1 hasta n),
las fórmulas de Faulhaber para la suma de las potencias de los primeros n números naturales o la suma de los cubos de tres números naturales consecutivos, cuyo valor es múltiplo de 9
|





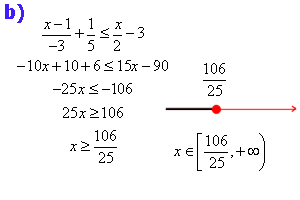

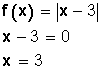


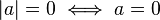



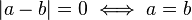



















No hay comentarios.:
Publicar un comentario