FUNCIONES
RESEÑA HISTORICA

Una breve historia de las funciones En las matemáticas actuales el concepto de función se define del modo siguiente: Sean A y B conjuntos. Se llama función entre A y B a cualquier relación establecida entre los elementos de A y B de tal modo que a cada elemento de A le corresponde un único elemento de B. 1 Para representar las funciones se suele utilizar la notación: f : A → B para los conjuntos, f(x) = y para los elementos A se llama conjunto inicial y B es el conjunto final f(x) = y se expresa como y es la imagen de x a través de la aplicación f. Se pueden definir funciones entre cualquier tipo de conjuntos, pero las más interesantes son las que se establecen entre conjuntos de números. En los próximos temas vamos a estudiar funciones definidas en el conjunto de los números reales: las funciones reales (conjunto final) de variable real (conjunto inicial), f : R → R . La pregunta que cabe hacerse ahora es: ¿cómo se ha llegado hasta aquí?. Es importante entender que el concepto se desarrolló con el paso del tiempo; su significado fue cambiando y también la forma en que se definía, ganando precisión a través de los años. Lo más apropiado, quizás, sea comenzar en Mesopotamia2 . En las matemáticas babilónicas encontramos tablas con los cuadrados, los cubos y los inversos de los números naturales. Estas tablas sin duda definen funciones de N en N o de N en R, lo que no implica que los babilonios conocieran el concepto de función. Conocían y manejaban funciones específicas, pero no el concepto abstracto y moderno de función3 . En el antiguo Egipto también aparecen ejemplos de usos de funciones particulares. Una tabla con la descomposición de 2/n en fracciones unitarias4 para los impares n desde 5 hasta 101 aparece en el Papiro Rhind o Papiro Ahmes, de unos 4000 años de antigüedad considerado como el primer tratado de matemáticas que se conserva.
RELACIONES Y FUNCIONES
PAR ORDENADOS :
Es un conjunto de dos elementos A y B que tiene un orden , A es primera componente y B es la segunda componente.
PRODUCTO CARTESIANO :
Sean A y B conjunto no vacios bamos a denominar producto cartesianoentre A y B al conjunto de todos los pares ordenados cuya primera componente perteneceal conjunto A y la segunda al conjunto B.

RELACION :
Es la correspondencia que se establece entre los elementos de los conjuntos A y B que no son vacios ,
donde conjunto A es punto de partida y B es punto de llegada.
DOMINIO DE UNA RELACION :
Son todos los elementos del conjunto de partida que tiene relacion con el conjunto de llegada y se la representa simbolicamente (don R ).
RANGO :
Son todos los elementos del conjunto de llegada que tiene relacion con el dominio del conjunto de parida , se o representa (rg R).
FUNCIONES :
- PUNTO : el dominio de toda relacion sea igual ha A.
X= independiente
Y= dependiente
TIPOS DE FUNCIONES :
- INYECTIVA : F es una funcion inyectiva si a cada elemento del rango es imagen exclusiva de un unico elemento del dominio ademas es necesario que N(A) sea MENOR o IGUAL a N(B) para poder construir esta funcion.
FUNCION SOBREYECTIVA : F es una funcion sobreyectiva si el rango de F es B , ademas es necesario que N(A) sea MAYOR o IGUAL que N(B).

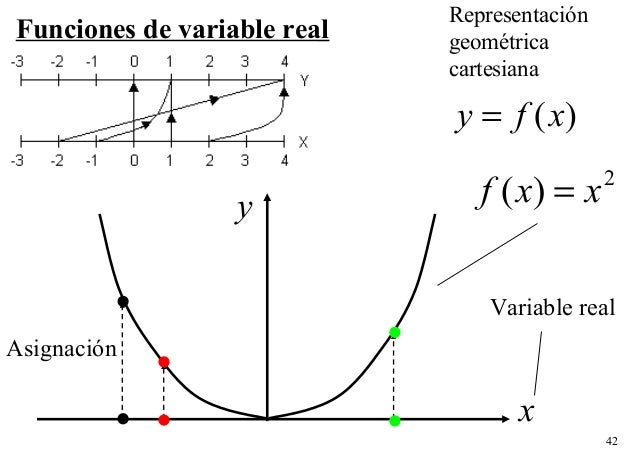
FUNCION DE VARIABLE REAL
Una función real  es una función matemática cuyo dominio y codominio están contenidos en el conjunto de los números reales denotado como
es una función matemática cuyo dominio y codominio están contenidos en el conjunto de los números reales denotado como  , es decir, es una función:
, es decir, es una función:
 es una función matemática cuyo dominio y codominio están contenidos en el conjunto de los números reales denotado como
es una función matemática cuyo dominio y codominio están contenidos en el conjunto de los números reales denotado como  , es decir, es una función:
, es decir, es una función:
En general se trata de funciones continuas, o bien discontinuas cuando están representadas por tramos, a diferencia de las funciones discretas, que son siempre discontinuas.
DOMINIO DE FUNCION DE VARIABLE REAL
Dada la función real de variable real f:A⊆R⟶R donde y=f(x) , llamamos dominio de f al conjunto A.
Es decir, A=Dom(f)={x∈R/∃f(x)}
Ejemplo:
Dada la función real de variable real f:A⊆R⟶R donde y=f(x)=x−2−−−−√ . Calcular el dominio de la función.
Planteamos la inecuación: x−2≥0
De donde se obtiene: x≥2
Así, el dominio de la función dada es: Domf={x∈R/x≥2}=[2,+∞[
RANGO DE FUNCION DE VARIABLE REAL
son los elementos de Y que se relacionan con X
ejemplo :

GRAFICA DE FUNCION DE VARIABLE REAL

Es el conjunto de puntos o pares ordenados de A x B ,tales que sus cordenadas (x,y) pertenecen a F.
EL CRITERIO DE LA RECTA VERTICAL
Una curva en el plano cartesiano representa una funcion si cualquier recta vertical intersecta la grafica, como maximo en un punto.

TIPOS DE FUNCIONES
Se dice que una
función es par si f(x) = f(-x), en el caso de que f(x) = -f(-x) se dice que la
función es impar.
Ejemplos 1:
La función y(x)=x
es impar ya que:
f(-x) = -x
pero
como f(x) = x entonces:
f(-x) = - f(x).

Ejemplo 2:
Otra función impar es y = 1/x
Cuando f(x) = -f(-x)
Ejemplo 3:
La función f(x)=x2
es par ya que f(-x) = (-x)2
=x2

Función estrictamente creciente en un intervalo
Una función
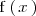 es estrictamente creciente en un intervalo
es estrictamente creciente en un intervalo
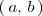 , si para dos valores cualesquiera del intervalo,
, si para dos valores cualesquiera del intervalo,
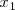 y
y
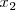 , se cumple que:
, se cumple que:
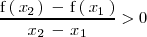

Cuando en la gráfica de una función estrictamente creciente nos movemos hacia la derecha tambien nos movemos hacia arriba:
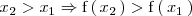
Una función
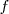 es estrictamente creciente en el punto de abcisa
es estrictamente creciente en el punto de abcisa
 si existe algun número positivo
si existe algun número positivo
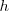 tal que
tal que
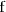 es estrictamente creciente en el intervalo
es estrictamente creciente en el intervalo
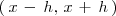 .
.
De esta esta definición se deduce que si
 es derivable en
es derivable en
 y
y
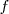 es estrictamente creciente en el punto de abcisa
es estrictamente creciente en el punto de abcisa
 , entonces
, entonces
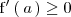 .
.
Función creciente en un intervalo
Una función
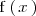 es creciente en un intervalo
es creciente en un intervalo
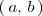 , si para dos valores cualesquiera del intervalo,
, si para dos valores cualesquiera del intervalo,
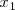 y
y
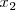 , se cumple que:
, se cumple que:
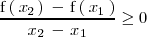
Función estrictamente decreciente en un intervalo
Una función
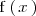 es estrictamente decreciente en un intervalo
es estrictamente decreciente en un intervalo
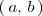 , si para dos valores cualesquiera del intervalo,
, si para dos valores cualesquiera del intervalo,
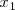 y
y
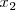 , se cumple que:
, se cumple que:
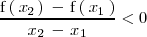
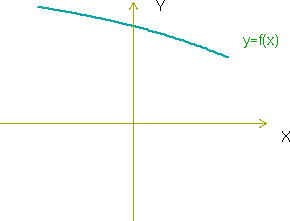
Cuando en la gráfica de una función estrictamente decreciente nos movemos hacia la derecha tambien nos movemos hacia abajo:
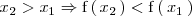
Una función
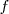 es estrictamente decreciente en el punto de abcisa
es estrictamente decreciente en el punto de abcisa
 si existe algun número positivo
si existe algun número positivo
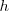 tal que
tal que
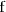 es estrictamente decreciente en el intervalo
es estrictamente decreciente en el intervalo
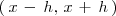 .
.
De esta esta definición se deduce que si
 es derivable en
es derivable en
 y
y
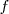 es estrictamente decreciente en el punto de abcisa
es estrictamente decreciente en el punto de abcisa
 , entonces
, entonces
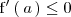 .
.
Función decreciente en un intervalo
Una función
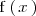 es decreciente en un intervalo
es decreciente en un intervalo
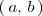 , si para dos valores cualesquiera del intervalo,
, si para dos valores cualesquiera del intervalo,
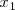 y
y
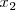 , se cumple que:
, se cumple que:
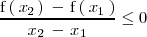
Funciones periódicas
Las funciones periódicas son funciones que se comportan en una manera cíclica (repetitiva) sobre un intervalo especificado (llamado un periodo). La gráfica se repite a si misma una y otra vez así como es trazada de izquierda a derecha. Enn otras palabras, la gráfica completa puede ser formada de copias de una porción particular, repetida en intervalos regulares indefinidamente. Si f es conocida sobre un periodo entonces es conocida en todas partes.Más formalmente, una función f es periódica si existe un número real P tal que f(x + P) = f(x) para todas las x.








 .
.




No hay comentarios.:
Publicar un comentario