MATRICES
RESEÑA HISTORICA
Evolución Histórica del Concepto de Matriz Antonio Rosales Góngora Anrogo58@yahoo.es Departamento de Matemáticas IES Bahía de Almería (España) Resumen Tratamos de hacer un recorrido histórico de la evolución del concepto de matriz, desde su aparición en el siglo XIX hasta su consolidación en el siglo XX. Conoceremos las aportaciones de Sylvester y Cayley, la escuela algebraica inglesa y las diversas interpretaciones hasta consolidar el concepto de matriz. Palabras claves:Historia de las matemáticas, matrices, álgebra. 1.1 Introducción Una matriz puede representar una tabla de valores, un determinante, una familia de vectores, una aplicación lineal, un endomorfismo, un sistema de ecuaciones diferenciales, una forma bilineal..., como podemos ver una misma representación matricial se puede interpretar de distintas maneras pero, también, diferentes matrices pueden representar el mismo objeto, por ejemplo, en los cambios de base de 2 Revista digital Matemática, Educación e I nternet (www.cidse.itcr.ac.cr/revistamate/). Vol 9, No 1. , 2008. las aplicaciones lineales. Pese a que, como dice Morris Kline ([9]), las matrices y determinantes no son un tema decisivo en la historia de las matemáticas porque, mas que nuevos contenidos teóricos, lo que aportan son innovaciones en el lenguaje o nuevos instrumentos de expresión matemática, no por ello debemos olvidar el lugar que han ocupado estas dimensiones en la evolución matemática. ¿La historia de la noción de matriz empieza en 1858 con la aparición de la memoria de Sylvester?¿Se remonta al cálculo de "cuadros" usado en el XIX desde Cauchy a Poincare?¿Debemos remontarnos en el tiempo y estudiar los sistemas de ecuaciones diferenciales lineales que ocupaban en el XVIII a D’Alambert, Lagrange y Laplace? En el siglo XX la idea de matriz se transformó en un elemento básico del álgebra. Se ha pasado de la idea original de Sylvester (1851) de matriz como madre de los menores de un determinante, por las leyes del cálculo de matrices de Cayley (1858), hasta los procedimientos de descomposición matricial de Weyr (1885). 1.2 ANTECEDENTES Los orígenes de las matrices y determinantes se encuentran entre los siglos II y III a.c. No nos debe sorprender su relación con el estudio de sistemas de ecuaciones lineales. En escritos babilonios aparece, sobre el 300 a.c. enunciados del tipo ([20]): "Tenemos dos campos con un área de 1800 yardas cuadradas. Uno produce grano en razón de 2 3 de celemín por yarda cuadrada, mientras que el otro lo hace en razón de 1 2 de celemín por yarda cuadrada. Si el total de la cosecha es de 1100 celemines ¿qué dimensiones tienen los campos?" Entre los años 200 y 100 a.c. aparece en China el libro "Nueve Capítulos sobre el Arte Matemático" , escrito durante la dinastía Han, que da el primer ejemplo conocido de método matricial. El problema es parecido al anterior: Evolución Histórica del Concepto de Matriz. Antonio Rosales Góngora. Derechos Reservados © 2009 Revista digital Matemática, Educación e Internet (www.cidse.itcr.ac.cr/revistamate/) Revista digital Matemática, Educación e I nternet (www.cidse.itcr.ac.cr/revistamate/). Vol 9, No 1. , 2008. 3 "Hay tres tipos de trigo, de los que tres sacos del primero, dos del segundo y uno del tercero hacen 39 medidas, dos del primero, tres del segundo y una del tercero son 34 medidas; una del primero, dos del segundo y tres del tercero son 26 medidas¿Cuántas medidas de cada tipo de trigo contiene un saco?" 1 2 3 2 3 2 3 1 1 26 34 39 El autor distribuye los coeficientes en una tabla e instruye como resolverlo con operaciones por columnas en lo que puede suponer el germen del método de Gauss. 0 0 3 4 5 2 8 1 1 39 24 39 El autor dice que multiplicando la primera columna por tres y restándola de la tercera es el camino más rápido, así como, multiplicar la columna central por tres y restarla de la de la derecha las veces posibles: El siguiente paso es multiplicar por 5 la última columna y entonces la columna central es restada de ella las veces posibles. 0 0 3 0 5 2 36 1 1 99 24 39 De aquí se puede obtener la solución por sustitución. Cardano en su "Ars Magna" (1545) da una regla para resolver sistemas de dos ecuaciones con dos incógnitas llamada "regula de modo" y que llama madre de las reglas. Esta regla es, esencialmente, el método de Cramer para sistemas de 2x2, salvo el último paso. Cardano no da la definición de determinante pero se encuentra latente. La idea de determinante aparece en Japón y Europa, más o menos, al mismo tiempo. En primer lugar, el japonés Seki, en 1683, escribe "Método para resolver los problemas disimulados" que contiene métodos escritos en tablas matriciales. Seki introduce los determinantes y da un método general para calcularlos, basado en ejemplos. Usando su "determinante", encuentra los determinantes de matrices de 2x2, 3x3, 4x4, 5x5 y los aplica para resolver ecuaciones aunque no sistemas de ecuaciones lineales. En el mismo año, 1683, Leibniz escribe a L’Hôpital, y le expone que el sistema de tres ecuaciones y dos incógnitas: 4 Revista digital Matemática, Educación e I nternet (www.cidse.itcr.ac.cr/revistamate/). Vol 9, No 1. , 2008. 10 + 11x + 12y = 0 20 + 21x + 22y = 0 30 + 31x + 32y = 0 Tiene solución porque 10 · 21 · 32 + 11 · 22 · 30 + 20 · 31 · 12 = 10 · 22 · 31 + 11 · 20 · 32 + 12 · 21 · 30 es decir, el determinante de la matriz de los coeficientes es nulo. Aquí Leibniz no usa coeficientes numéricos, pues, estaba convencido, que una buena notación era la llave para el progreso, y experimentó con distintas notaciones hasta expresarlo de esta manera, donde 21 denota nuestro actual a21. Leibniz usó el término "Resultante" para ciertas sumas combinatorias de términos del determinante e incluso, estudia sistemas de coeficientes de formas cuadráticas, que lo empujaron hacia las matrices. No obstante, fue Maclaurin quien, en su libro póstumo, Treatise of Algebra (con resultados obtenidos probablemente en el año 1729, y publicados en 1748) usó el método de los determinantes para resolver sistemas de ecuaciones lineales con 2, 3 y 4 incógnitas (con 4, dejó planteado o sugerido el método). Aquí se encuentra la llamada "regla de Cramer". Si se tiene el sistema ax + by = c dx + ey = f , la solución viene dada por y = a f − dc ae − db . Y si el sistema es ax + by + cz = m dx + ey + f z = n gx + hy + f z = p entonces: z = aep − ahn + dhm − dbp + gbn − gem aek − ah f + dhc − dbk + gb f − gec Cramer, tratando de encontrar la ecuación de una curva plana que pasara por un número dado de puntos, encontró su regla, publicada en 1750 en "Introduction á l’analyses des lignes courbes algebraiques". Bezout, en 1764, mostró que en un sistema lineal homogéneo de n ecuaciones con n incógnitas, tiene soluciones no nulas si el determinante de los coeficientes se anula. De la misma forma, Vandermonde en 1771 ofrece una exposición consistente
CLASES DE MATRICES
DEFINICION DE MATRICES : Una matriz real A es un arreglo rectangular de numeros reales , en donde cada elemento Aij que pertenece a la matriz A tiene dos subindices . el subindice i representa la fila que es la horizontal , y el subindice j representa la columna que es la vertical , en las cuales se encuentra el elemento.
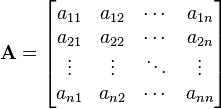
CLASIFICACION Y PROPIEDADES DE MATRICES
Triangular superior
En una matriz triangular superior los elementos situados por debajo de la diagonal principal son ceros.
En una matriz triangular superior los elementos situados por debajo de la diagonal principal son ceros.
Triangular inferior
En una matriz triangular inferior los elementos situados por encima de la diagonal principal son ceros
Diagonal
En una matriz diagonal todos los elementos situados por encima y por debajo de la diagonal principal son nulos.
En una matriz diagonal todos los elementos situados por encima y por debajo de la diagonal principal son nulos.
Escalar
Una matriz escalar es una matriz diagonal en la que los elementos de la diagonal principal son iguales.
Una matriz escalar es una matriz diagonal en la que los elementos de la diagonal principal son iguales.
Identidad
Una matriz identidad es una matriz diagonal en la que los elementos de la diagonal principal son iguales a 1.
Una matriz identidad es una matriz diagonal en la que los elementos de la diagonal principal son iguales a 1.
Potencia
Se llama potencia k-ésima de una matriz cuadrada A, donde k OE Õ, un entero positivo, al producto de A por sí misma, repetido k veces.
Ak =A⋅A⋅A⋅......k veces ...... ⋅A
Se conviene en que:
A- k = (A- 1) k " k OE Õ
A0 = I
Periodica
Se llama potencia k-ésima de una matriz cuadrada A, donde k OE Õ, un entero positivo, al producto de A por sí misma, repetido k veces.
Ak =A⋅A⋅A⋅......k veces ...... ⋅A
Se conviene en que:
A- k = (A- 1) k " k OE Õ
A0 = I
Periodica
si
 . Si p es el menor número natural que satisface
. Si p es el menor número natural que satisface  , entonces decimos que A es una matriz periódica de período
, entonces decimos que A es una matriz periódica de período
Nilpotente
Si A es una matriz cuadrada y Ak = 0 para algún número natural k, se dice que A es nilpotente. Si k es tal que Ak −1 ≠ 0 y Ak = 0, se dice que A es nilpotente de orden k.
Idempotente
Una matriz, A, es idempotente si:
A2 = A.
Involutiva
Una matriz, A, es involutiva si:
A2 = I.
Traspuesta
Dada una matriz A, se llama matriz traspuesta de A a la matriz que se obtiene cambiando ordenadamente las filas por las columnas
Si A es una matriz cuadrada y Ak = 0 para algún número natural k, se dice que A es nilpotente. Si k es tal que Ak −1 ≠ 0 y Ak = 0, se dice que A es nilpotente de orden k.
Idempotente
Una matriz, A, es idempotente si:
A2 = A.
Involutiva
Una matriz, A, es involutiva si:
A2 = I.
Traspuesta
Dada una matriz A, se llama matriz traspuesta de A a la matriz que se obtiene cambiando ordenadamente las filas por las columnas
(At)t = A
(A + B)t = At + Bt
(α ·A)t = α· At
(A · B)t = Bt · At
Simétrica
Una matriz simétrica es una matriz cuadrada que verifica:
A = At.
Antisimetrica
Una matriz antisimétrica o hemisimétrica es una matriz cuadrada que verifica:
A = -At.
Compleja
Sus elementos son números complejos aij e ¬
Conjugada
Matriz conjugada de una matriz A Aquella que se obtiene sustituyendo cada elemento por su complejo conjugado (igual parte real, pero la parte imaginaria cambiada de signo)
Hermitiana o hermitica
Una matriz hermitiana (o hermítica) es una matriz cuadrada de elementoscomplejos que tiene la característica de ser igual a su propia traspuestaconjugada. Es decir, el elemento en la i-ésima fila y j-ésima columna es igual al conjugado del elemento en la j-ésima fila e i-ésima columna, para todos los índices i y j:

(A + B)t = At + Bt
(α ·A)t = α· At
(A · B)t = Bt · At
Simétrica
Una matriz simétrica es una matriz cuadrada que verifica:
A = At.
Antisimetrica
Una matriz antisimétrica o hemisimétrica es una matriz cuadrada que verifica:
A = -At.
Compleja
Sus elementos son números complejos aij e ¬
Conjugada
Matriz conjugada de una matriz A Aquella que se obtiene sustituyendo cada elemento por su complejo conjugado (igual parte real, pero la parte imaginaria cambiada de signo)
Hermitiana o hermitica
Una matriz hermitiana (o hermítica) es una matriz cuadrada de elementoscomplejos que tiene la característica de ser igual a su propia traspuestaconjugada. Es decir, el elemento en la i-ésima fila y j-ésima columna es igual al conjugado del elemento en la j-ésima fila e i-ésima columna, para todos los índices i y j:

o, escrita con la traspuesta conjugada A*:
es una matriz hermítica.
Antihermitiana
una Matriz antihermitiana es una matriz cuadrada cuya traspuesta conjugada es menos la matriz. Esto es si satisface a la relación:
A * = -A
Antihermitiana
una Matriz antihermitiana es una matriz cuadrada cuya traspuesta conjugada es menos la matriz. Esto es si satisface a la relación:
A * = -A
o en su forma componente, si (A = ai,j):
Para todas las i y las j.
Ortogonal
Una matriz ortogonal es necesariamente cuadrada e invertible : A-1 = AT La inversa de una matriz ortogonal es una matriz ortogonal. El producto de dos matrices ortogonales es una matriz ortogonal. El determinante de una matriz ortogonal vale +1 ó -1.
OPERACIONES ENTRE MATRICES
IGUALDAD DE MATRICES
Definición:
Dos matrices son iguales si tienen las mismas dimensiones y cada elemento de la primera es igual al elemento de la segunda que ocupa su misma posición. Es decir:
Ejemplo:

SUMA DE MATRICES
Definición.
Sean  Mm,n dos matrices dimensión m x n. La suma de A con B es otra matriz C también de dimensión m x n definida por:
Mm,n dos matrices dimensión m x n. La suma de A con B es otra matriz C también de dimensión m x n definida por: 
Ejemplo: 

RESTA DE MATRICES
Definición.
Sean  Mm,n dos matrices de la misma dimensión. Se define la matriz
Mm,n dos matrices de la misma dimensión. Se define la matriz  como la suma de
como la suma de  con la opuesta de
con la opuesta de  . Es decir,
. Es decir,
PRODUCTO DE MATRICES
Definición.
Dadas las matrices A de dimensión m x n y B de dimensión n x p se define la matriz producto C de dimensión m x p como aquella cuyo elemento  se obtiene multiplicando la i-esima fila de la matriz A por la k-esima columna de la matriz B. Es decir:
se obtiene multiplicando la i-esima fila de la matriz A por la k-esima columna de la matriz B. Es decir:
 ,
, 
Para poder multiplicar dos matrices tiene que verificarse que el no de columnas de la primera coincida con el no de filas de la segunda.
Ejemplo:


Es decir, la matriz C quedaría:

POTENCIA DE UNA MATRIZ
Potencia de una matriz de orden 3
Resolver matriz potencia. Con este guión puedes calcular la potencia de una matriz de orden 3, muy útil para calcular por inducción una matriz elevada a n.
Utilización guión matriz potencia

DETERMINANTES
DETERMINANTE DE UNA MATRIZ
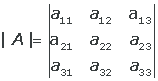 =
=
= a11 a22 a33 + a12 a23 a 31 + a13 a21 a32 -
- a 13 a22 a31 - a12 a21 a 33 - a11 a23 a32.
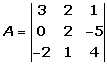 =
=
3 · 2 · 4 + 2 · (-5) · (-2) + 1 · 0 · 1 -
- 1 · 2 · (-2) - 2 · 0 · 4 - 3 · (-5) · 1 =
= 24 + 20 + 0 - (-4) - 0 - (-15) =
= 44 + 4 + 15 = 63
Obsérvese que hay seis productos, cada uno de ellos formado por tres elementos de la matriz. Tres de los productos aparecen con signo positivo (conservan su signo) y tres con signo negativo (cambian su signo).
Regla de Sarrus
La regla de Sarrus es una utilidad para calcular determinantes de orden 3.
Los términos con signo + están formados por los elementos de la diagonal principal y los de lasdiagonales paralelas con su correspondiente vértice opuesto.

Los términos con signo - están formados por los elementos de la diagonal secundaria y los de lasdiagonales paralelas con su correspondiente vértice opuesto.

Ejemplo

METODOS PARA ENCONTRAR LA DETERMINANTE DE UNA MATRIZ








 = a 11 a 22 − a 12 a 21
= a 11 a 22 − a 12 a 21







 =
= 