MATRICES

                                                RESEÑA HISTORICA







                                               



Evolución Histórica del Concepto de Matriz Antonio Rosales Góngora Anrogo58@yahoo.es Departamento de Matemáticas IES Bahía de Almería (España) Resumen Tratamos de hacer un recorrido histórico de la evolución del concepto de matriz, desde su aparición en el siglo XIX hasta su consolidación en el siglo XX. Conoceremos las aportaciones de Sylvester y Cayley, la escuela algebraica inglesa y las diversas interpretaciones hasta consolidar el concepto de matriz. Palabras claves:Historia de las matemáticas, matrices, álgebra. 1.1 Introducción Una matriz puede representar una tabla de valores, un determinante, una familia de vectores, una aplicación lineal, un endomorfismo, un sistema de ecuaciones diferenciales, una forma bilineal..., como podemos ver una misma representación matricial se puede interpretar de distintas maneras pero, también, diferentes matrices pueden representar el mismo objeto, por ejemplo, en los cambios de base de 2 Revista digital Matemática, Educación e I nternet (www.cidse.itcr.ac.cr/revistamate/). Vol 9, No 1. , 2008. las aplicaciones lineales. Pese a que, como dice Morris Kline ([9]), las matrices y determinantes no son un tema decisivo en la historia de las matemáticas porque, mas que nuevos contenidos teóricos, lo que aportan son innovaciones en el lenguaje o nuevos instrumentos de expresión matemática, no por ello debemos olvidar el lugar que han ocupado estas dimensiones en la evolución matemática. ¿La historia de la noción de matriz empieza en 1858 con la aparición de la memoria de Sylvester?¿Se remonta al cálculo de "cuadros" usado en el XIX desde Cauchy a Poincare?¿Debemos remontarnos en el tiempo y estudiar los sistemas de ecuaciones diferenciales lineales que ocupaban en el XVIII a D’Alambert, Lagrange y Laplace? En el siglo XX la idea de matriz se transformó en un elemento básico del álgebra. Se ha pasado de la idea original de Sylvester (1851) de matriz como madre de los menores de un determinante, por las leyes del cálculo de matrices de Cayley (1858), hasta los procedimientos de descomposición matricial de Weyr (1885). 1.2 ANTECEDENTES Los orígenes de las matrices y determinantes se encuentran entre los siglos II y III a.c. No nos debe sorprender su relación con el estudio de sistemas de ecuaciones lineales. En escritos babilonios aparece, sobre el 300 a.c. enunciados del tipo ([20]): "Tenemos dos campos con un área de 1800 yardas cuadradas. Uno produce grano en razón de 2 3 de celemín por yarda cuadrada, mientras que el otro lo hace en razón de 1 2 de celemín por yarda cuadrada. Si el total de la cosecha es de 1100 celemines ¿qué dimensiones tienen los campos?" Entre los años 200 y 100 a.c. aparece en China el libro "Nueve Capítulos sobre el Arte Matemático" , escrito durante la dinastía Han, que da el primer ejemplo conocido de método matricial. El problema es parecido al anterior: Evolución Histórica del Concepto de Matriz. Antonio Rosales Góngora. Derechos Reservados © 2009 Revista digital Matemática, Educación e Internet (www.cidse.itcr.ac.cr/revistamate/) Revista digital Matemática, Educación e I nternet (www.cidse.itcr.ac.cr/revistamate/). Vol 9, No 1. , 2008. 3 "Hay tres tipos de trigo, de los que tres sacos del primero, dos del segundo y uno del tercero hacen 39 medidas, dos del primero, tres del segundo y una del tercero son 34 medidas; una del primero, dos del segundo y tres del tercero son 26 medidas¿Cuántas medidas de cada tipo de trigo contiene un saco?" 1 2 3 2 3 2 3 1 1 26 34 39 El autor distribuye los coeficientes en una tabla e instruye como resolverlo con operaciones por columnas en lo que puede suponer el germen del método de Gauss. 0 0 3 4 5 2 8 1 1 39 24 39 El autor dice que multiplicando la primera columna por tres y restándola de la tercera es el camino más rápido, así como, multiplicar la columna central por tres y restarla de la de la derecha las veces posibles: El siguiente paso es multiplicar por 5 la última columna y entonces la columna central es restada de ella las veces posibles. 0 0 3 0 5 2 36 1 1 99 24 39 De aquí se puede obtener la solución por sustitución. Cardano en su "Ars Magna" (1545) da una regla para resolver sistemas de dos ecuaciones con dos incógnitas llamada "regula de modo" y que llama madre de las reglas. Esta regla es, esencialmente, el método de Cramer para sistemas de 2x2, salvo el último paso. Cardano no da la definición de determinante pero se encuentra latente. La idea de determinante aparece en Japón y Europa, más o menos, al mismo tiempo. En primer lugar, el japonés Seki, en 1683, escribe "Método para resolver los problemas disimulados" que contiene métodos escritos en tablas matriciales. Seki introduce los determinantes y da un método general para calcularlos, basado en ejemplos. Usando su "determinante", encuentra los determinantes de matrices de 2x2, 3x3, 4x4, 5x5 y los aplica para resolver ecuaciones aunque no sistemas de ecuaciones lineales. En el mismo año, 1683, Leibniz escribe a L’Hôpital, y le expone que el sistema de tres ecuaciones y dos incógnitas: 4 Revista digital Matemática, Educación e I nternet (www.cidse.itcr.ac.cr/revistamate/). Vol 9, No 1. , 2008. 10 + 11x + 12y = 0 20 + 21x + 22y = 0 30 + 31x + 32y = 0 Tiene solución porque 10 · 21 · 32 + 11 · 22 · 30 + 20 · 31 · 12 = 10 · 22 · 31 + 11 · 20 · 32 + 12 · 21 · 30 es decir, el determinante de la matriz de los coeficientes es nulo. Aquí Leibniz no usa coeficientes numéricos, pues, estaba convencido, que una buena notación era la llave para el progreso, y experimentó con distintas notaciones hasta expresarlo de esta manera, donde 21 denota nuestro actual a21. Leibniz usó el término "Resultante" para ciertas sumas combinatorias de términos del determinante e incluso, estudia sistemas de coeficientes de formas cuadráticas, que lo empujaron hacia las matrices. No obstante, fue Maclaurin quien, en su libro póstumo, Treatise of Algebra (con resultados obtenidos probablemente en el año 1729, y publicados en 1748) usó el método de los determinantes para resolver sistemas de ecuaciones lineales con 2, 3 y 4 incógnitas (con 4, dejó planteado o sugerido el método). Aquí se encuentra la llamada "regla de Cramer". Si se tiene el sistema ax + by = c dx + ey = f , la solución viene dada por y = a f − dc ae − db . Y si el sistema es    ax + by + cz = m dx + ey + f z = n gx + hy + f z = p entonces: z = aep − ahn + dhm − dbp + gbn − gem aek − ah f + dhc − dbk + gb f − gec Cramer, tratando de encontrar la ecuación de una curva plana que pasara por un número dado de puntos, encontró su regla, publicada en 1750 en "Introduction á l’analyses des lignes courbes algebraiques". Bezout, en 1764, mostró que en un sistema lineal homogéneo de n ecuaciones con n incógnitas, tiene soluciones no nulas si el determinante de los coeficientes se anula. De la misma forma, Vandermonde en 1771 ofrece una exposición consistente


                                                 CLASES DE MATRICES

DEFINICION DE MATRICES : Una matriz real A es un arreglo rectangular de numeros reales , en donde cada elemento Aij que pertenece a la matriz A tiene dos subindices . el subindice i representa la fila que es la horizontal , y el subindice j representa la columna que es la vertical , en las cuales se encuentra el elemento.




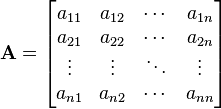
CLASIFICACION Y PROPIEDADES DE MATRICES

Triangular superior
En una matriz triangular superior los elementos situados por debajo de la diagonal principal son ceros.

Triangular inferior

En una matriz triangular inferior los elementos situados por encima de la diagonal principal son ceros

Diagonal
En una matriz diagonal todos los elementos situados por encima y por debajo de la diagonal principal son nulos.

Escalar

Una matriz escalar es una matriz diagonal en la que los elementos de la diagonal principal son iguales.

Identidad

Una matriz identidad es una matriz diagonal en la que los elementos de la diagonal principal son iguales a 1.

Potencia

Se llama potencia k-ésima de una matriz cuadrada A, donde k OE Õ, un entero positivo, al producto de A por sí misma, repetido k veces.

Ak =A⋅A⋅A⋅......k veces ...... ⋅A

Se conviene en que:

A- k = (A- 1) k " k OE Õ

A0 = I

Periodica

si  . Si p es el menor número natural que satisface , entonces decimos que A es una matriz periódica de período

Nilpotente

Si A es una matriz cuadrada y Ak = 0 para algún número natural k, se dice que A es nilpotente. Si k es tal que Ak −1 ≠ 0 y Ak = 0, se dice que A es nilpotente de orden k.

Idempotente

Una matriz, A, es idempotente si:

A2 = A.

Involutiva
Una matriz, A, es involutiva si:

A2 = I.

Traspuesta
Dada una matriz A, se llama matriz traspuesta de A a la matriz que se obtiene cambiando ordenadamente las filas por las columnas

(At)t = A
(A + B)t = At + Bt
(α ·A)t = α· At
(A · B)t = Bt · At
Simétrica
Una matriz simétrica es una matriz cuadrada que verifica:

A = At.
Antisimetrica
Una matriz antisimétrica o hemisimétrica es una matriz cuadrada que verifica:
A = -At.

Compleja

Sus elementos son números complejos aij e ¬

Conjugada

Matriz conjugada de una matriz A Aquella que se obtiene sustituyendo cada elemento por su complejo conjugado (igual parte real, pero la parte imaginaria cambiada de signo)
Hermitiana o hermitica
Una matriz hermitiana (o hermítica) es una matriz cuadrada de elementoscomplejos que tiene la característica de ser igual a su propia traspuestaconjugada. Es decir, el elemento en la i-ésima fila y j-ésima columna es igual al conjugado del elemento en la j-ésima fila e i-ésima columna, para todos los índices i y j:

o, escrita con la traspuesta conjugada A*:

Por ejemplo,

es una matriz hermítica.

Antihermitiana 

una Matriz antihermitiana es una matriz cuadrada cuya traspuesta conjugada es menos la matriz. Esto es si satisface a la relación:

A * = -A

o en su forma componente, si (A = ai,j):

Para todas las i y las j.

Ortogonal
Una matriz ortogonal es necesariamente cuadrada e invertible : A-1 = AT La inversa de una matriz ortogonal es una matriz ortogonal. El producto de dos matrices ortogonales es una matriz ortogonal. El determinante de una matriz ortogonal vale +1 ó -1.

       

                                       OPERACIONES ENTRE MATRICES

IGUALDAD DE MATRICES

Definición:

Dos matrices son iguales si tienen las mismas dimensiones y cada elemento de la primera es igual al elemento de la segunda que ocupa su misma posición. Es decir:

M_m,n  

Ejemplo:

SUMA DE MATRICES

     Definición.

Sean M_m,n dos matrices dimensión  m x n. La suma de A con B es otra matriz C también de dimensión  m x  n definida por:  

Ejemplo: 

RESTA DE MATRICES

     Definición.

Sean M_m,n dos matrices de la misma dimensión. Se define la matriz  como la suma de  con la opuesta de . Es decir,

PRODUCTO DE MATRICES

     Definición.

Dadas las matrices A de dimensión  m x n  y B de dimensión  n x p  se define la matriz producto C de dimensión  m x  p  como aquella cuyo elemento  se obtiene multiplicando la i-esima fila de la matriz A por la k-esima columna de la matriz B. Es decir:

  M_m,p ;  , 

Para poder multiplicar dos matrices tiene que verificarse que el n^o de columnas de la primera coincida con el n^o de filas de la segunda.

Ejemplo:

Es decir, la matriz C quedaría:

POTENCIA DE UNA MATRIZ

Potencia de una matriz de orden 3

Resolver matriz potencia. Con este guión puedes calcular la potencia de una matriz de orden 3, muy útil para calcular por inducción una matriz elevada a n.

Utilización guión matriz potencia

                                               DETERMINANTES

DETERMINANTE DE UNA MATRIZ

 =

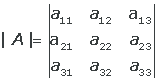= a₁₁ a₂₂ a₃₃ + a₁₂ a₂₃ a ₃₁ + a₁₃ a₂₁ a₃₂ -

- a ₁₃ a₂₂ a₃₁ - a₁₂ a₂₁ a ₃₃ - a₁₁ a₂₃ a_32.

 =

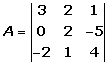3 · 2 · 4 + 2 · (-5) · (-2) + 1 · 0 · 1 -

- 1 · 2 · (-2) - 2 · 0 · 4 - 3 · (-5) · 1 =

= 24 + 20 + 0 - (-4) - 0 - (-15) =

= 44 + 4 + 15 = 63

Obsérvese que hay seis productos, cada uno de ellos formado por tres elementos de la matriz. Tres de los productos aparecen con signo positivo (conservan su signo) y tres con signo negativo (cambian su signo).

Regla de Sarrus

La regla de Sarrus es una utilidad para calcular determinantes de orden 3.

Los términos con signo + están formados por los elementos de la diagonal principal y los de lasdiagonales paralelas con su correspondiente vértice opuesto.

Los términos con signo - están formados por los elementos de la diagonal secundaria y los de lasdiagonales paralelas con su correspondiente vértice opuesto.

Ejemplo

METODOS PARA ENCONTRAR LA DETERMINANTE DE UNA MATRIZ

Determinante de orden uno

  |a₁₁| = a₁₁

Ejemplo

  |−2| = −2

Determinante de orden dos

 = a ₁₁ a ₂₂ − a ₁₂ a ₂₁

Ejemplo 

Determinante de orden tres

Se aplica la regla de Sarrus:

Ejemplo 

Cálculo de un determinante de cualquier orden

Consiste en conseguir que una de las líneas del determinante esté formada por elementos nulos, menos uno: el elemento base o pivote, que valdrá 1 ó −1.

Seguiremos los siguientes pasos:

 1  Si algún elemento del determinante vale la unidad, se elige una de las dos líneas: la fila o la columna, que contienen a dicho elemento (se debe escoger aquella que contenga el mayor número posible de elementos nulos).

 2  En caso negativo seguiremos alguno de los siguientes pasos:

 1.  Nos fijamos en una línea que contenga el mayor número posible de elementos nulos y operaremos para que uno de los elementos de esa línea sea un 1 ó un −1 (operando con alguna línea paralela).

 2.   Dividiendo la línea fila (o la columna) por uno de sus elementos, por lo cual deberíamos multiplicar el determinante por dicho elemento para que su valor no varie. Es decir, sacamos factor común en una fila (o una columna) de uno de sus elementos.

 3  Tomando como referencia el elemento base, operaremos de modo que todos los elementos de la fila o columna, donde se encuentre, sean ceros.

 4  Tomamos el adjunto del elemento base, con lo que obtenemos un determinante de orden inferior en una unidad al original.

 = 2(−58)= − 116

                                             NUMEROS COMPLEJOS

         
                                                   Reseña historica

         

                                          


Breve historia de los N´umeros Complejos Teniendo conocimiento de c´omo la raza humana ha adquirido su sabidur´ıa sobre ciertos hechos y conceptos, estaremos en mejor disposici´on de juzgar c´omo los ni˜nos adquieren tal conocimiento. George P´olya (1887-1985) Primeras referencias: SI-SXII La primera referencia escrita de la ra´ız cuadrada de un n´umero negativo la encontramos en la obra Stereometr´ıa de Her´on de Alejandr´ıa (Greciaaprox. 10-75) alrededor de la mitad del siglo I. Es este trabajo comparece la operaci´on √81 − 144 aunque es tomada como √144 − 81, no sabi´endose si este error es debido al propio Her´on o al personal encargado de transcribirlo. La siguiente referencia sobre esta cuesti´on se data en el a˜no 275 en la obra de Diophantus (aprox. 200-284) Arithmetica. En su intento de c´alculo de los lados de un tri´angulo rect´angulo de per´ımetro 12 y ´area 7, Diophantus plante´o resolver la ecuaci´on 336x2 + 24 = 172x, ecuaci´on de ra´ıces complejas como puede ser comprobado f´acilmente. Son los matem´aticos hind´ues los que dan las primeras explicaciones a este tipo de problemas. Mahavira, alrededor del a˜no 850, comenta en su tratado de los n´umeros negativos que ”como en la naturaleza de las cosas una catidad negativa no es un cuadrado, por tanto no puede tener ra´ız cuadrada”. Alrededor de 1150 es Bhaskara quien lo describe de la siguiente forma: El cuadrado de un n´umero, positivo o negativo, es positivo; la ra´ız cuadrada de un n´umero positivo tiene dos valores, uno positivo y otro negativo; no existe ra´ız cuadrada de un n´umero negativo ya que un n´umero negativo no es un cuadrado. Primeros estudios: SXVI J. Cardan (1501 - 1576) En 1545, Jerome Cardan (Italia, 1501-1576), un matem´atico, f´ısico y fil´osofo italiano, publica ”Ars Magna” (El Gran Arte) en el cual describe un m´etodo para resolver ecuaciones algebraicas de grado tres y cuatro. Esta obra se convert´ıa as´ı en el mayor tratado de ´algebra desde los Babil´onicos, 3000 a˜nos antes, que dedujeron c´omo resolver la ecuaci´on cuadr´atica. Un problema planteado por Cardan en su trabajo es el siguiente: An´alisis Matem´atico VI - Curso 2006/2007 Breve historia de los N´umeros Complejos 2 Si alguien te pide dividir 10 en dos partes cuyos producto sea... 40, es evidente que esta cuesti´on es imposible. No obstante, nosotros la resolvemos de la siguiente forma. Cardan aplicaba entonces su algoritmo al sistema de ecuaciones x + y = 10, xy = 40 dando como soluciones 5 + √−15 y 5 − √−15. Por multiplicaci´on probaba Cardan que el producto era 40. Esta es la primera constancia escrita de la ra´ız de un n´umero negativo y de su manejo algebraico. Cardan tambi´en tropieza con estas ra´ıces en las soluciones que presenta de la ecuaci´on c´ubica x3 = ax + b. Tales soluciones vienen dadas por: x = 3 b 2 + b 2 2 − a 3 3 + 3 b 2 − b 2 2 − a 3 3 . Para la ecuaci´on x3 = 15x + 4 esta f´ormula da como soluci´on x = 3 2 + √−121 + 3 2 − √−121, la cual Cardan di´o por v´alida. Como esta ecuaci´on tiene las ra´ıces 4, −2+√ 3 y −2−√ 3, interesaba la relaci´on con las propuestas por la f´ormula de Cardan. Fu´e el ingeniero hidra´ulico Rafael Bombelli (Italia, 1526 - 1572), unos treinta a˜nos despu´es de la publicaci´on de la obra de Cardan, quien introdujo un razonamiento que el mismo catalog´o de un tanto ”salvaje”. Plante´o que como −2 + √−121 y −2−√−121 s´olo se diferencian en un signo, lo mismo deb´ıa suceder con sus ra´ıces c´ubicas. As´ı escrib´ıa 3 −2 + √−121 = a + √ −b y 3 −2 − √ −121 = a − √ −b, donde por c´alculo directo obten´ıa que a =2y b = 1, luego 3 −2 + √ −121 + 3 −2 − √ −121 = (2 + √ −1) + (2 + √ −1) = 4. As´ı Bombelli ”daba sentido” a las expresiones ”sin sentido” de Cardan. Este razonamiento se convierte por tanto como el nacimiento de la variable compleja. Bombelli desarroll´o un c´alculo de operaciones con n´umeros complejos que se ajusta a los que conocemos en la actualidad. Comentar en este punto que comunmente se dice que fu´e la ecuaci´on cuadr´atica la que forz´o la definici´on de los n´umeros complejos. Con lo expuesto anteriormente debemos asignar a la ecuaci´on de orden tres tal papel. A pesar de lo aportado por Bombelli, su trabajo sobre esta materia (L’Algebra) fu´e ampliamente ignorado y considerado como misterioso e incierto. Sim´on Stevin apunt´o en 1585 lo siguiente en esta direcci´on: Tiene toda la legitimidad el que uno se ejercite en otras tareas y no pierda el tiempo en inexactitudes. Dos siglos y medio cubrieron las dudas sobre el significado y la autenticidad de los n´umeros complejos. No obstante, fueron estudiados por un gran n´umero de matem´aticos.

                                                 REPRESENTACIONES

 Definicion de un numero complejo

Los números complejos conforman un grupo de cifras resultantes de la suma entre un número real y uno de tipo imaginario. Un número real, de acuerdo a la definición, es aquel que puede ser expresado por un número entero (4, 15, 2686) o decimal (1,25; 38,1236; 29854,152). En cambio, un número imaginario es aquél cuyo cuadrado es negativo. El concepto de número imaginario fue desarrollado por Leonhard Euler en 1777, cuando le otorgó a v-1 el nombre de i (de “imaginario”).

FORMAS RECTANGULAR DE UN NUMERO COMPLEJO

 

Representación geométrica de un número complejo.Sea z = a + b·i un número complejo en forma binómica. Su expresión en forma cartesiana es
z = (a,b). Consideremos el plano euclídeo real R², y en él un sistema de referencia ortonormal. A cada número complejo z = a + b·i le hacemos corresponder un punto del plano P(a,b); y recíprocamente, dado ese punto del plano le asociamos el complejo z = a + b·i. Tenemos pues una biyección entre el plano euclídeo real R² y el cuerpo de los núneros complejos C.
 

 

El punto del plano P(a,b) correspondiente al complejo z = a + b·i recibe el nombre de afijo de z. El ángulo que forma el vector OP con el eje de abcisas recibe el nombre de argumento de z.
Además, el módulo del vector OP es:

|OP| = (a² + b²)^1/2 = |z|

que coincide con la distancia del punto P al origen de coordenadas. 

 

Sea r = |z|. Si x es su argumento, se tiene que:

sen x = PA/OP = b/r ==> b = r·sen x
cos x = OA/OP = a/r ==> a = r·cos x Luego podernos escribir z = a + b·i = r·cos x + i·r·sen x = r·(cos x + i·sen x) 

---

Forma trigonométrica y forma polar.

Esta expresión, z = r·(cos x + i·sen x), recibe el nombre de forma trigonométrica de z, donde r es el módulo de z y x su argumento. 
Definimos la forma polar del número complejo z = r·(cos x + i·sen x) como r_x. 

---

Igualdad de números complejos en forma trigonométrica.

Veamos cuando dos complejos en forma trigonométrica, o en forma polar, son iguales: 
Sean z₁ = r·(cos x + i·sen x) y z₂ = r´·(cos y + i·sen y). Si z₁ = z₂, entonces r·(cos x + i·sen x) = r´·(cos y + i·sen y). Como dos números complejos iguales tienen el mismo módulo, entonces r = r´, y por tanto, (cos x + i·sen x) = (cos y + i·sen y), de donde:

cos x = cos y	==> y = x + 2·k·pi, con k C Z
sen x = sen y

Por tanto, r·(cos x + i·sen x) = r·[cos (x + 2·k·pi) + i·sen(x + 2·k·pi)], y en forma polar resulta: r_x = r_{x + 2·k·pi}

---

Paso de la forma binómica a la forma polar

Hemos visto que z = a + b·i = r·(cos x + i·sen x) = r·cos x + i·r·senx, de donde:

a = r·cos x

b = r·sen x

Por otra parte, sea z = a + b·i un número complejo en forma binómica. Por definición tenemos que: |z| = (a² + b²)^1/2 Además es: b/a = (r·sen x)/(r·cos x) = (sen x)/(cos x) = tg x Por tanto x = arc tg (b/a) estudiando el cuadrante de x según los signos de la parte real y de la parte imaginaria le z.

El numero complejo x+0i generalmente se escribe como (x) y representa un numero real (Q) , en cambioel numero complejo 0+yi generalmente se escribe (yi) y representa un numero imaginario puro.

Re (z) | x real

Im (z) | y imaginario

Conjugado de un número complejo

Se llama conjugado de un número complejo al número complejo que se obtiene por simetría del dado respecto del eje de abscisas.

Representando el número complejo a + bi  y haciendo la correspondiente simetría, se tiene que su conjugado es a - bi .

Dado un número complejo, su conjugado puede representarse poniendo encima del mismo una línea horizontal. Así se escribirá:

                                           

CARACTERISTICAS DE LAS POTENCIAS DE LOS IMAGINARIOS

En la potenciación de números imaginarios, existen equivalencias e identidades que serían las siguientes:

i⁰=1

i¹=i

i²=-1

i³=-i

i⁴=1

Estas notaciones se van repitiendo cada cuatro números, lo cual quiere decir que para saber cuál es un determinado valor de la potencia de un número imaginario o complejo, debemos dividir el exponente entre cuatro y el resto del exponente es la potencia equivalente según las identidades notables que anotamos anteriormente.

EJEMPLO

Por ejemplo: i²⁶

Tomamos 26 y dividimos para 4, lo que nos da: 6×4+2=26

Sabiendo entonces que 2 es el exponente indicado según su equivalencia, decimos que:

i²⁶ = (i⁴)⁶ × i² = 1⁶ × -1 = -1

Intenta averiguar cuál es el resultado de i²⁷.

                                                                  OPERACIONES

Igualdad de números complejos. Opuesto y conjugado.

Dos números complejos son iguales si lo son las partes reales e imaginarias respectivamente: a+bi=a'+b'i          ⇔        a=a'    y     b=b'   Dado el número complejo  z=a+bi  se define: su opuesto como el número complejo  −z=−a−bi su conjugado como el número complejo   z ¯ =a−bi Observa que el opuesto de z es simétrico a z respecto del origen conjugado de z es simétrico a z respecto al eje X.                                                   Ejemplos de las propiedades de la suma Propiedad cerrada: 3i + 4i = 7i. Propiedad conmutativa: 2i + 4i = 4i + 2i. Propiedad distributiva: (6i + 4i) × 5i = (6i ×5i) + (4i × 5i). Número neutro: 8i + 0 = 8i. Elemento opuesto o inverso aditivo: 3i -3i = 0. Ejemplos en el producto o multiplicación Propiedad conmutativa: (6i) (3i) = (3i) (6i) o lo que es lo mismo 6i × 3i = 3i × 6i. Propiedad distributiva: 3i × (5i × 4i) = (3i × 5i) × 4i. Elemento opuesto o Inverso multiplicativo: 4i × 1/4i = 1. Ejemplo de las propiedades de la potenciación Unidad imaginaria: √-1 = i. Esta es la propiedad que define al número imaginario i. Operaciones con números imaginarios Suma Para hacer operaciones con números imaginarios, en este caso la suma, seguimos las reglas básicas de la matemática agrupando los números reales y los números imaginarios respectivamente. (a+bi)+(c+di)=(a+c)+(b+d)i Como ejemplo tenemos: (5+3i)+(2+6i) = (5+2)+(3i+6i) = 7+9i Sustracción Para realizar la sustracción, también se deben agrupar los números imaginarios y reales. Por ejemplo: (5-2i)-(2+6i) = (5-2)+(-2i-6i) = 3-8i Multiplicación Para la multiplicación debemos multiplicar cada término del primer factor por los del segundo. (a+bi)(c+di) = ac+adi+bci+bdi² = (ac-bd)+(ad+bc)i Podemos observar que el elemento bdi² se convierte en –bd por la propiedad de los números imaginarios en la cual i² es igual a -1. Como ejemplo tenemos: (3+2i)(6+7i) = 18+21i+12i+14i² = (18-14)+(21+12)i = 4+33i